X 2 X 3 2
catronauts
Sep 11, 2025 · 5 min read
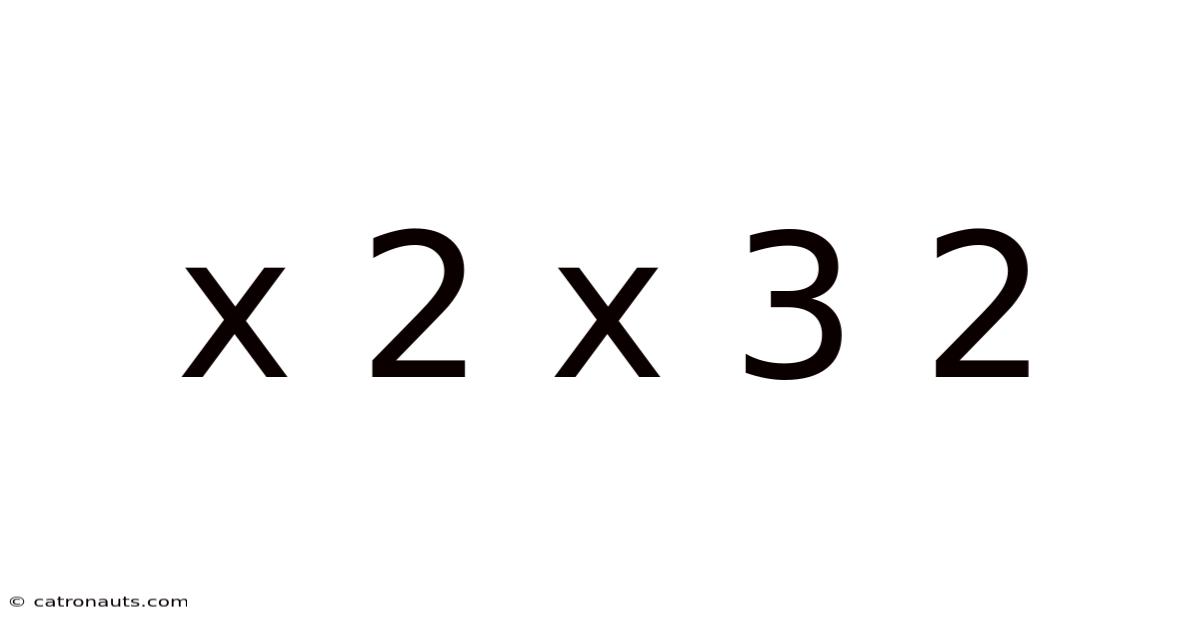
Table of Contents
Decoding x² x³ x²: Exploring the Fundamentals of Algebraic Expressions and their Applications
This article delves into the seemingly simple algebraic expression x² x³ x², exploring its underlying principles, simplification methods, and practical applications in various fields. Understanding this expression lays a crucial foundation for grasping more complex algebraic concepts and their real-world implications. We'll break down the expression step-by-step, clarifying the rules of exponents and demonstrating how to simplify and manipulate such expressions. By the end, you'll not only be able to solve this specific expression but also confidently tackle similar algebraic challenges.
Introduction: Understanding the Basics
Before diving into the intricacies of x² x³ x², let's establish a strong base. This expression involves variables (represented by 'x') and exponents (the small numbers written above the variables, indicating repeated multiplication). Understanding these two key elements is critical.
A variable, in mathematics, is a symbol (usually a letter) that represents an unknown or unspecified number. In our case, 'x' is the variable. The value of 'x' can change, making it versatile in representing various mathematical situations.
An exponent indicates how many times a base number (or variable) is multiplied by itself. For example:
- x² means x * x (x multiplied by itself)
- x³ means x * x * x (x multiplied by itself three times)
Therefore, x² x³ x² represents (x * x) * (x * x * x) * (x * x).
Simplifying the Expression: The Rules of Exponents
Simplifying x² x³ x² involves applying the fundamental rules of exponents, specifically the product of powers rule. This rule states that when multiplying two or more terms with the same base, we add their exponents.
Let's apply this rule to our expression:
x² x³ x² = x⁽²⁺³⁺²⁾ = x⁷
Therefore, the simplified form of x² x³ x² is x⁷. This means x multiplied by itself seven times.
Explanation of the Steps: A Detailed Breakdown
Let's break down the simplification process step-by-step to reinforce understanding:
-
Identify the base: In our expression, the base is 'x'. This is the common element that allows us to apply the product of powers rule.
-
Identify the exponents: The exponents are 2, 3, and 2, respectively.
-
Apply the product of powers rule: Since we're multiplying terms with the same base, we add the exponents: 2 + 3 + 2 = 7
-
Write the simplified expression: The simplified expression is x⁷.
Beyond the Basics: Exploring Other Exponent Rules
The product of powers rule is just one of several crucial exponent rules. Understanding these rules is essential for mastering algebraic manipulation. Let's briefly touch upon other important rules:
-
Power of a power rule: (xᵃ)ᵇ = xᵃᵇ. This rule states that when raising a power to another power, we multiply the exponents. For example, (x²)³ = x⁶.
-
Quotient of powers rule: xᵃ / xᵇ = x⁽ᵃ⁻ᵇ⁾. This rule explains that when dividing terms with the same base, we subtract the exponents. For example, x⁵ / x² = x³.
-
Power of a product rule: (xy)ᵃ = xᵃyᵃ. This rule indicates that when raising a product to a power, we raise each factor to that power. For example, (xy)² = x²y².
-
Power of a quotient rule: (x/y)ᵃ = xᵃ/yᵃ. Similar to the power of a product rule, this applies when raising a quotient to a power. For example, (x/y)³ = x³/y³.
-
Zero exponent rule: x⁰ = 1 (where x ≠ 0). Any base raised to the power of zero equals 1.
-
Negative exponent rule: x⁻ᵃ = 1/xᵃ. A negative exponent indicates the reciprocal of the base raised to the positive exponent. For example, x⁻² = 1/x².
Practical Applications: Where Does This Matter?
The seemingly simple algebraic manipulation demonstrated here—simplifying x² x³ x²—has wide-ranging applications across various fields:
-
Physics: Many physical laws and equations involve exponents. Calculating velocity, acceleration, or the force of gravity often requires manipulating expressions with exponents.
-
Engineering: Engineering disciplines, from civil to electrical, heavily rely on mathematical modeling. Simplifying complex algebraic expressions, including those with exponents, is crucial for solving engineering problems.
-
Computer Science: Algorithms and data structures frequently involve exponential growth or decay. Understanding exponent rules is vital for analyzing the efficiency of algorithms and managing data structures.
-
Finance: Compound interest calculations, determining the future value of investments, and understanding exponential growth in financial markets all require working with exponential expressions.
-
Chemistry: Chemical reactions and calculations often involve exponents when describing reaction rates and concentrations.
-
Biology: Population growth, decay of radioactive substances, and other biological processes can be modeled using exponential functions.
Frequently Asked Questions (FAQ)
-
What if the bases were different? If the bases were different (e.g., x² y³ z²), we couldn't directly simplify the expression using the product of powers rule. Each term would remain separate.
-
What if there were negative exponents? Negative exponents would be handled using the negative exponent rule (x⁻ᵃ = 1/xᵃ) before applying the product of powers rule. For example, x⁻² x³ x⁴ would be simplified as follows: (1/x²) * x³ * x⁴ = x⁵.
-
Can I use a calculator to simplify this? While a scientific calculator can handle exponent calculations, understanding the underlying principles is crucial for solving more complex algebraic problems. Calculators are tools, not replacements for understanding mathematical concepts.
-
What if the expression involved parentheses? Parentheses indicate order of operations (PEMDAS/BODMAS). Simplify the expressions within parentheses first before applying the exponent rules.
Conclusion: Mastering Algebraic Expressions
The seemingly simple expression x² x³ x² provides a powerful gateway to understanding fundamental algebraic concepts. Mastering the rules of exponents is crucial for tackling more complex mathematical problems in various fields. By systematically applying the product of powers rule, we successfully simplified x² x³ x² to x⁷. Remember that this foundational knowledge extends far beyond this specific example, forming the bedrock for more advanced algebraic manipulations and their real-world applications. Practice applying these rules and exploring various examples to build your confidence and mastery of algebraic expressions. The more you practice, the more intuitive these concepts will become. Don't be afraid to experiment and challenge yourself with increasingly complex expressions. The journey of learning mathematics is a rewarding one, filled with the satisfaction of solving problems and unlocking the secrets of the universe.
Latest Posts
Latest Posts
-
Popular Rhythm And Blues Songs
Sep 12, 2025
-
Little Red Riding Hood Book
Sep 12, 2025
-
Formula For Appreciation And Depreciation
Sep 12, 2025
-
What Is The Public Sector
Sep 12, 2025
-
What Is Vertically Opposite Angles
Sep 12, 2025
Related Post
Thank you for visiting our website which covers about X 2 X 3 2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.