X 3 2x 2 X
catronauts
Sep 13, 2025 · 6 min read
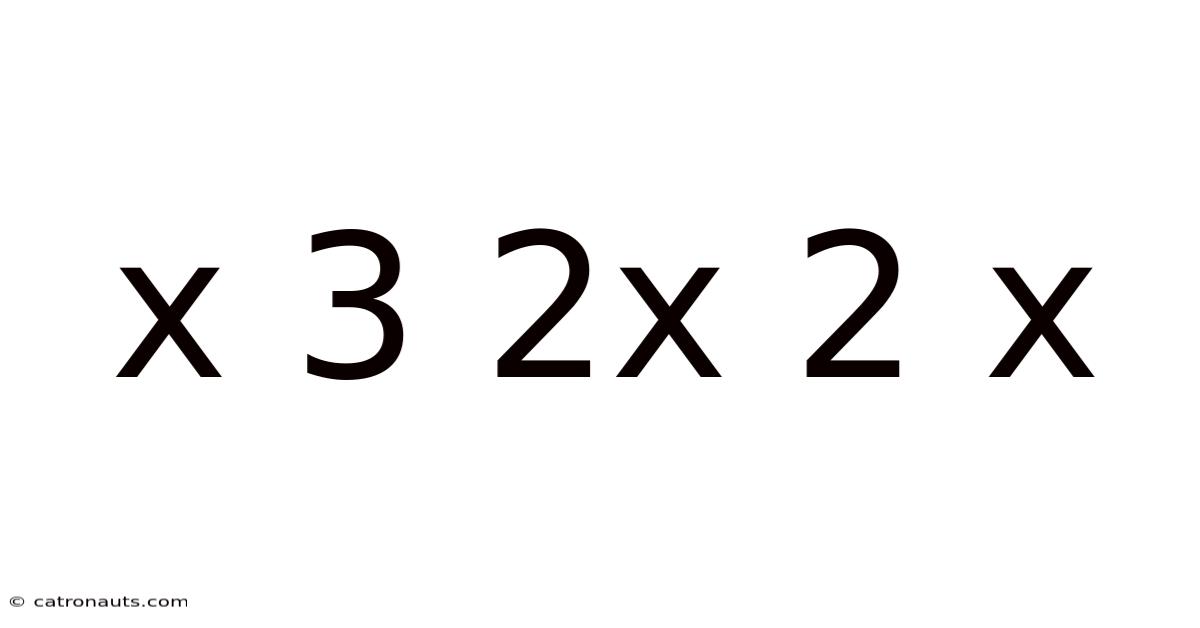
Table of Contents
Decoding the Mathematical Expression: x³ + 2x² + x
This article delves into the mathematical expression x³ + 2x² + x, exploring its components, potential solutions, and practical applications. We'll unpack its meaning, examine different approaches to solving related problems, and discuss its relevance in various fields. Understanding this seemingly simple equation opens doors to a deeper appreciation of algebra and its uses in the real world. This exploration will be beneficial for students learning algebra, those brushing up on their math skills, and anyone curious about the elegance and power of mathematical expressions.
Understanding the Components
The expression x³ + 2x² + x is a polynomial. Specifically, it's a cubic polynomial because the highest power of the variable x is 3. Let's break down each term:
- x³: This represents x multiplied by itself three times (x * x * x). It's a cubic term.
- 2x²: This term represents 2 multiplied by x multiplied by itself (2 * x * x). It's a quadratic term.
- x: This is a linear term, simply representing the variable x itself (or 1*x).
The entire expression is the sum of these three terms. The coefficients (the numbers in front of the variables) are 1 (for x³), 2 (for 2x²), and 1 (for x). The absence of a constant term (a number without an x) is noteworthy.
Solving for x: Finding the Roots
Solving for x means finding the values of x that make the entire expression equal to zero. This is finding the roots or zeros of the polynomial. There are several ways to approach this:
1. Factoring: This is often the most straightforward method if the polynomial can be easily factored. In this case, we can factor out an x:
x³ + 2x² + x = x(x² + 2x + 1)
Notice that the expression in the parentheses is a perfect square trinomial: (x + 1)(x + 1) or (x + 1)². Therefore, the fully factored form is:
x(x + 1)² = 0
This equation is satisfied when either x = 0 or (x + 1)² = 0. The latter simplifies to x = -1. Therefore, the roots of the polynomial are x = 0 and x = -1 (with a multiplicity of 2 for x = -1).
2. Using the Cubic Formula: For more complex cubic polynomials that don't factor easily, the cubic formula can be used. However, this formula is quite lengthy and complicated, and it's generally less efficient than factoring when factoring is possible. The cubic formula is not typically taught at the introductory algebra level due to its complexity.
3. Numerical Methods: For cubic polynomials that are difficult or impossible to factor, numerical methods such as the Newton-Raphson method can be used to approximate the roots. These methods use iterative calculations to get closer and closer to the actual roots. These methods are usually employed with the help of computers or calculators.
4. Graphical Methods: Plotting the function y = x³ + 2x² + x will show where the graph intersects the x-axis. These intersection points represent the roots of the polynomial. This method provides a visual representation of the solutions and is particularly useful for understanding the behavior of the function.
Practical Applications
Cubic polynomials, like x³ + 2x² + x, appear in numerous real-world applications across various fields:
-
Physics: Cubic equations can model the trajectory of projectiles, the oscillations of certain systems, and the relationship between variables in various physical phenomena. For example, the motion of a damped harmonic oscillator might involve a cubic equation.
-
Engineering: In structural engineering, cubic equations can be used to model the deflection of beams under load. In electrical engineering, cubic polynomials can represent the characteristics of certain circuits or components.
-
Chemistry and Biology: Cubic equations can model reaction rates, population growth, and other dynamic processes in chemical and biological systems. For instance, the growth of a certain bacteria population might follow a cubic growth model under specific conditions.
-
Economics: Cubic functions can sometimes be used to model cost functions, revenue functions, or other economic relationships, although other models are often more appropriate for complex economic scenarios.
-
Computer Graphics and Animation: Cubic curves (curves described by cubic equations) are used extensively in computer-aided design (CAD) and computer graphics to create smooth and realistic curves and shapes. Bézier curves, a fundamental tool in computer graphics, are often defined by cubic polynomials.
Further Exploration: Variations and Extensions
The expression x³ + 2x² + x is a foundational example. Let's consider variations and extensions:
-
Adding a constant term: If we add a constant term (e.g., x³ + 2x² + x + 5 = 0), factoring becomes more challenging, and numerical or graphical methods might be necessary to find the roots. The addition of a constant term shifts the graph vertically.
-
Changing the coefficients: Altering the coefficients (the numbers 1, 2, and 1) will change the shape and location of the graph, thereby changing the roots of the polynomial. Different coefficients lead to different solutions.
-
Higher-order polynomials: The principles discussed here extend to polynomials of higher degrees (e.g., quartic, quintic, etc.). However, finding the roots becomes increasingly complex as the degree of the polynomial increases. While factoring might still be possible in some cases, numerical methods often become essential for higher-order polynomials.
Frequently Asked Questions (FAQ)
Q: What is the difference between a root and a zero of a polynomial?
A: The terms "root" and "zero" are used interchangeably. They both refer to the values of x that make the polynomial equal to zero.
Q: Can a cubic polynomial have more than three roots?
A: No, a cubic polynomial (a polynomial of degree 3) can have at most three real roots. It can also have complex roots (roots involving imaginary numbers), but the total number of roots (including real and complex roots) will always be three.
Q: Is there a general formula for solving quartic (degree 4) polynomials?
A: Yes, there is a general formula for solving quartic polynomials, but it's even more complicated than the cubic formula. For polynomials of degree 5 or higher, there is no general algebraic formula for finding the roots.
Q: How do I know which method to use to solve a cubic equation?
A: The best method depends on the specific cubic equation. If it can be easily factored, factoring is generally the easiest and most efficient method. Otherwise, numerical or graphical methods might be necessary.
Conclusion
The expression x³ + 2x² + x, while seemingly simple, offers a rich entry point into the world of algebra and its applications. Understanding its components, how to find its roots, and its relevance in various fields provides a strong foundation for further mathematical exploration. Whether you're a student grappling with algebra or a curious individual seeking to deepen your understanding of mathematics, mastering concepts like this unlocks the door to a more profound appreciation for the power and elegance of mathematical expressions. Remember, the journey of learning is a continuous process, and every step, no matter how small, brings you closer to a deeper understanding of the world around us.
Latest Posts
Latest Posts
-
How Old Is Brian Maddox
Sep 13, 2025
-
Adding Fractions With Similar Denominators
Sep 13, 2025
-
Citric Acid With Sodium Bicarbonate
Sep 13, 2025
-
Periodic Inventory Vs Perpetual Inventory
Sep 13, 2025
-
Diorama Of An Animal Habitat
Sep 13, 2025
Related Post
Thank you for visiting our website which covers about X 3 2x 2 X . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.