1 3 Of 250 Ml
catronauts
Sep 11, 2025 · 6 min read
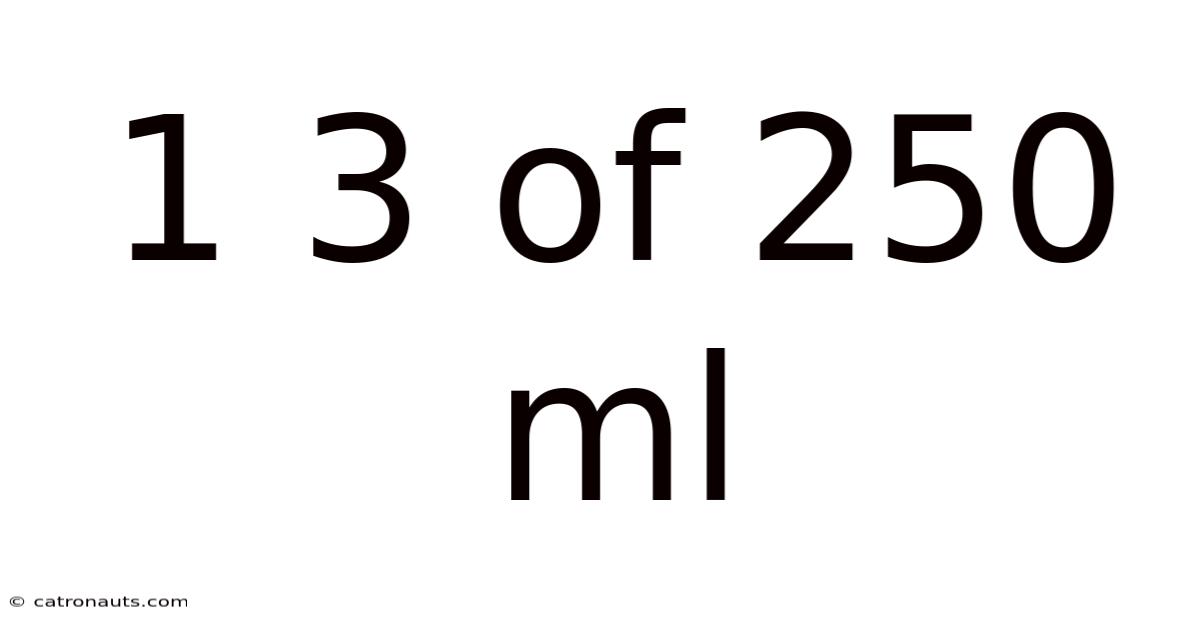
Table of Contents
Decoding 1/3 of 250ml: A Comprehensive Guide to Fraction Calculations and Practical Applications
Understanding fractions is a fundamental skill in mathematics, crucial for everyday life and advanced studies. This article delves into the seemingly simple problem of calculating 1/3 of 250ml, exploring the underlying mathematical principles, providing step-by-step solutions, and extending the concept to broader applications. Whether you're a student struggling with fractions, a cook needing precise measurements, or simply curious about the practical use of mathematics, this guide will equip you with the knowledge and confidence to tackle similar problems. We will cover various methods for calculating fractions, ensuring you understand the process and can apply it in diverse contexts.
Understanding the Problem: 1/3 of 250ml
The question "What is 1/3 of 250ml?" asks us to find one-third of a quantity. This involves dividing the total quantity (250ml) into three equal parts and taking one of those parts. The problem directly relates to the concept of fractions and their application in measurement and proportion. The keyword here is "fraction," which is a crucial element for understanding this calculation. This calculation appears simple at first glance but provides a valuable opportunity to illustrate different approaches to fraction calculations and their practical relevance.
Method 1: Direct Calculation Using Multiplication
The most straightforward method involves converting the fraction to a decimal and then multiplying. We know that 1/3 is approximately equal to 0.333 (recurring). Therefore, we can calculate 1/3 of 250ml as follows:
0.333 * 250ml ≈ 83.25ml
This method is quick and efficient for simple calculations, but it introduces a slight inaccuracy due to the rounding off of the decimal representation of 1/3. The recurring decimal nature of 1/3 means that this result is an approximation.
Method 2: Fraction Multiplication
A more precise method involves performing fraction multiplication directly:
(1/3) * 250ml = 250/3 ml
This fraction can then be simplified:
250/3 ml ≈ 83.333... ml
This gives a more accurate result than the decimal approximation in Method 1. However, the answer is still a recurring decimal, representing an infinite series of 3s. For practical purposes, you'd likely round this to 83.3ml. The use of fractions here ensures precision and allows us to understand the exact mathematical relationship.
Method 3: Division
Alternatively, we can approach this problem using division. Since we want to find one-third of 250ml, we simply divide 250 by 3:
250ml / 3 ≈ 83.333... ml
This method directly addresses the core concept of finding one part out of three equal parts. Again, the result is a recurring decimal, underscoring the exact nature of the calculation and highlighting the limitations of decimal representation for certain fractions. This method reinforces the concept of fractions as representing division.
Understanding the Remainder
The recurring decimal in the answers from Methods 2 and 3 highlights an important concept: the remainder. When dividing 250 by 3, we get 83 with a remainder of 1. This remainder represents the portion of 1ml that is not equally distributed among the three parts. In practical terms, this remainder might be negligible, or it might require a different approach depending on the context. For instance, if you are dividing a liquid among three containers, you might choose to add the extra 1ml to one of the containers, making the division slightly uneven.
Practical Applications: Beyond the Calculation
The seemingly simple calculation of 1/3 of 250ml has extensive applications in various fields:
-
Cooking and Baking: Precise measurements are critical in culinary arts. Recipes often require fractions of specific ingredients. Knowing how to calculate fractions is vital to achieving consistent and successful results. For example, understanding 1/3 of 250ml of milk could be crucial in a recipe.
-
Science and Engineering: Fractions are fundamental in scientific calculations and engineering designs. Determining proportions, concentrations, or ratios frequently involves fraction calculations. For instance, calculating the volume of a specific chemical component in a solution might require understanding this concept.
-
Everyday Life: From dividing resources equally among family members to calculating discounts and sales, the ability to handle fractions is a valuable life skill. Understanding portion sizes or sharing tasks equally relies on your proficiency in fractions.
-
Finance and Business: Percentage calculations, essential in finance and business, rely heavily on fractions. Understanding discounts, interest rates, or profit margins requires working with fractions and their decimal equivalents. This is a crucial skill for anyone working with financial statements or managing budgets.
-
Construction and Carpentry: Precise measurements are essential in construction and carpentry. Calculating lengths, angles, and material quantities requires a deep understanding of fractions and ratios. This ensures that projects are completed accurately and efficiently.
Expanding the Concept: Other Fractions of 250ml
Let's extend this understanding to other fractions of 250ml:
-
1/2 of 250ml: This is a simpler calculation, resulting in 125ml (250ml / 2 = 125ml).
-
2/3 of 250ml: This is double the result of 1/3 of 250ml. It would be approximately 166.67ml (250ml/3 * 2).
-
1/4 of 250ml: This equals 62.5ml (250ml / 4 = 62.5ml)
These examples demonstrate how understanding the basic principles allows you to easily calculate various fractions of a given quantity. Each calculation involves either multiplication or division, with the ability to convert between fractions and decimals providing flexibility in the approach.
Frequently Asked Questions (FAQ)
Q1: Why is 1/3 a recurring decimal?
A1: The decimal representation of 1/3 is 0.333... because 1 divided by 3 does not result in a finite decimal. It's a rational number that cannot be expressed as a simple terminating decimal.
Q2: Which method is most accurate for calculating 1/3 of 250ml?
A2: Method 2 (fraction multiplication) and Method 3 (division) offer greater accuracy than Method 1 (decimal approximation) because they avoid rounding errors introduced when using the approximate decimal value of 1/3. While the result is still a recurring decimal, it represents the exact mathematical solution.
Q3: How do I handle the remainder in real-world applications?
A3: In practical situations, the remainder can be handled in several ways: you can round up or down depending on the context, distribute it unevenly, or consider it a negligible amount depending on the required precision. The best approach depends on the specific situation and the degree of accuracy needed.
Q4: Can I use a calculator for these calculations?
A4: Yes, a calculator can simplify the calculations, especially for more complex fractions. However, understanding the underlying mathematical principles remains crucial for interpreting the results and applying the concepts effectively in various situations.
Conclusion: Mastering Fractions for a Brighter Future
Calculating 1/3 of 250ml provides a clear example of how fundamental mathematical concepts apply to everyday situations. By understanding the different methods for calculating fractions—whether through direct multiplication, fraction multiplication, or division—you gain valuable problem-solving skills with broad applications across diverse fields. Mastering fractions is not just about getting the right answer; it's about developing a deeper understanding of proportion, ratio, and the relationship between fractions and decimals. This skill empowers you to tackle more complex problems and enhances your critical thinking abilities, making it an invaluable asset in your personal and professional life. Remember, the key is not just to perform the calculation but to understand the underlying principles and apply them confidently and effectively.
Latest Posts
Latest Posts
-
Is A Spider And Insect
Sep 11, 2025
-
Very Beautiful In French Language
Sep 11, 2025
-
How To Factorise Cubic Functions
Sep 11, 2025
-
X 2 X 3 2
Sep 11, 2025
-
O Captain My Captain Film
Sep 11, 2025
Related Post
Thank you for visiting our website which covers about 1 3 Of 250 Ml . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.