15 75 As A Percentage
catronauts
Sep 12, 2025 · 5 min read
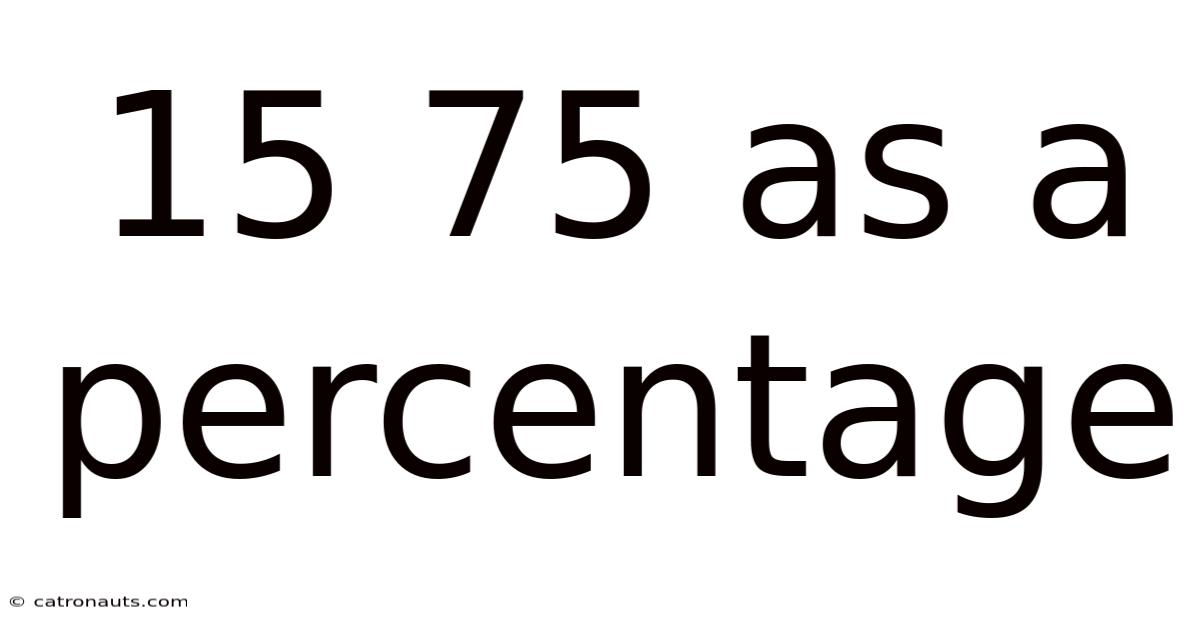
Table of Contents
15/75 as a Percentage: A Comprehensive Guide
Understanding how to convert fractions to percentages is a fundamental skill in mathematics with widespread applications in everyday life, from calculating discounts in shops to understanding financial reports. This article will provide a comprehensive guide to calculating 15/75 as a percentage, explaining the process step-by-step and exploring the underlying mathematical principles. We'll also delve into practical applications and address frequently asked questions to solidify your understanding.
Introduction: Understanding Percentages
A percentage is a way of expressing a number as a fraction of 100. The term "percent" literally means "out of 100" ( per cent). Therefore, 15/75 as a percentage means finding what proportion of 100 15 represents when compared to 75. This conversion is crucial in various fields, from calculating grades to determining profit margins and understanding statistical data. Knowing how to perform this conversion efficiently and accurately is essential for anyone dealing with numerical data.
Method 1: Simplifying the Fraction
The simplest way to convert 15/75 to a percentage involves first simplifying the fraction to its lowest terms. This makes the subsequent calculation much easier.
-
Find the Greatest Common Divisor (GCD): The GCD of 15 and 75 is 15. This means both numbers are divisible by 15 without leaving a remainder.
-
Divide both the numerator and the denominator by the GCD:
15 ÷ 15 = 1 75 ÷ 15 = 5
-
Simplified Fraction: This simplifies our fraction to 1/5.
-
Convert to a Percentage: To convert a fraction to a percentage, we multiply the fraction by 100%.
(1/5) * 100% = 20%
Therefore, 15/75 simplifies to 1/5, which is equivalent to 20%.
Method 2: Direct Calculation
Alternatively, you can directly convert the fraction to a percentage without simplifying first. This method is useful when the GCD isn't immediately apparent.
-
Convert the Fraction to a Decimal: Divide the numerator (15) by the denominator (75):
15 ÷ 75 = 0.2
-
Multiply by 100%: To convert the decimal to a percentage, multiply by 100%:
0.2 * 100% = 20%
This confirms that 15/75 is indeed equal to 20%. Both methods yield the same result, demonstrating the flexibility of percentage calculations.
Method 3: Using Proportions
Another approach to solving this problem is to use proportions. We can set up a proportion to find the equivalent percentage:
15/75 = x/100
To solve for x (the percentage), we cross-multiply:
15 * 100 = 75 * x
1500 = 75x
x = 1500 ÷ 75
x = 20
Therefore, x = 20%, confirming our previous calculations. This method highlights the relationship between fractions and percentages as equivalent representations of the same proportion.
Practical Applications of Percentage Calculations
The ability to calculate percentages has numerous real-world applications across various domains:
-
Academic Performance: Students frequently use percentages to understand their grades, representing the proportion of correctly answered questions or the overall performance in a subject. For example, if a student answers 15 out of 75 questions correctly, their score is 20%.
-
Financial Management: Percentages are crucial in finance for calculating interest rates, discounts, profit margins, tax rates, and investment returns. Understanding these percentages helps in making informed financial decisions.
-
Sales and Marketing: Businesses use percentages to represent discounts, sales tax, and profit margins. For example, a 20% discount on an item helps customers understand the price reduction.
-
Data Analysis and Statistics: Percentages are extensively used to represent proportions in data analysis and statistics. For example, market share or the percentage of people holding a particular opinion can be represented using percentages.
-
Everyday Life: Percentages are commonplace in various everyday scenarios, from calculating tips at restaurants to understanding nutritional information on food labels.
Explanation of the Mathematical Concepts
The conversion from a fraction to a percentage involves understanding the relationship between fractions, decimals, and percentages. All three represent proportions, but in different forms.
-
Fractions: Fractions represent a part of a whole, expressed as a numerator (the top number) divided by a denominator (the bottom number). In our example, 15/75 represents 15 parts out of a total of 75 parts.
-
Decimals: Decimals are another way to represent fractions, where the denominator is a power of 10 (e.g., 10, 100, 1000). The decimal equivalent of 15/75 is 0.2.
-
Percentages: Percentages represent a fraction as parts per hundred. The percentage is found by multiplying the decimal equivalent by 100.
The core mathematical concept underpinning the conversion is the principle of proportionality. We maintain the same ratio between the numerator and the denominator while scaling the fraction to a denominator of 100. This allows for easy comparison and interpretation of proportions.
Frequently Asked Questions (FAQs)
-
Q: Can I use a calculator to convert 15/75 to a percentage?
A: Yes, you can. Simply divide 15 by 75 and then multiply the result by 100. Most calculators have a percentage function that streamlines this process.
-
Q: What if the fraction doesn't simplify easily?
A: If the fraction doesn't simplify easily, you can still use the direct calculation method (dividing the numerator by the denominator and multiplying by 100) or the proportion method.
-
Q: Why is understanding percentages important?
A: Understanding percentages is important because it's a crucial skill for interpreting and analyzing numerical information in various contexts, making it essential for academic success, financial literacy, and daily decision-making.
-
Q: Are there any online tools or websites that can help with percentage calculations?
A: While I cannot provide links to external websites, a simple online search for "percentage calculator" will reveal numerous free tools that can help you perform these calculations.
Conclusion: Mastering Percentage Conversions
Converting fractions to percentages is a fundamental mathematical skill that is applicable in numerous real-world situations. By understanding the underlying principles and employing the methods outlined in this article, you can confidently convert any fraction to a percentage. Whether you use the simplification method, direct calculation, or proportions, the result will always be the same: 15/75 equals 20%. Mastering this skill will significantly enhance your ability to analyze data, make informed decisions, and navigate various numerical challenges in your personal and professional life. Remember that practice is key to building fluency and confidence in performing these calculations. Try working through different fraction-to-percentage conversions to solidify your understanding and enhance your mathematical skills.
Latest Posts
Latest Posts
-
Compound Interest Formula In Excel
Sep 12, 2025
-
What Is Net Realizable Value
Sep 12, 2025
-
Is Wrist Distal To Elbow
Sep 12, 2025
-
Lewis Dot Structure For Chcl3
Sep 12, 2025
-
Difference Between Transparent And Translucent
Sep 12, 2025
Related Post
Thank you for visiting our website which covers about 15 75 As A Percentage . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.