2 000 Divided By 12
catronauts
Sep 13, 2025 · 5 min read
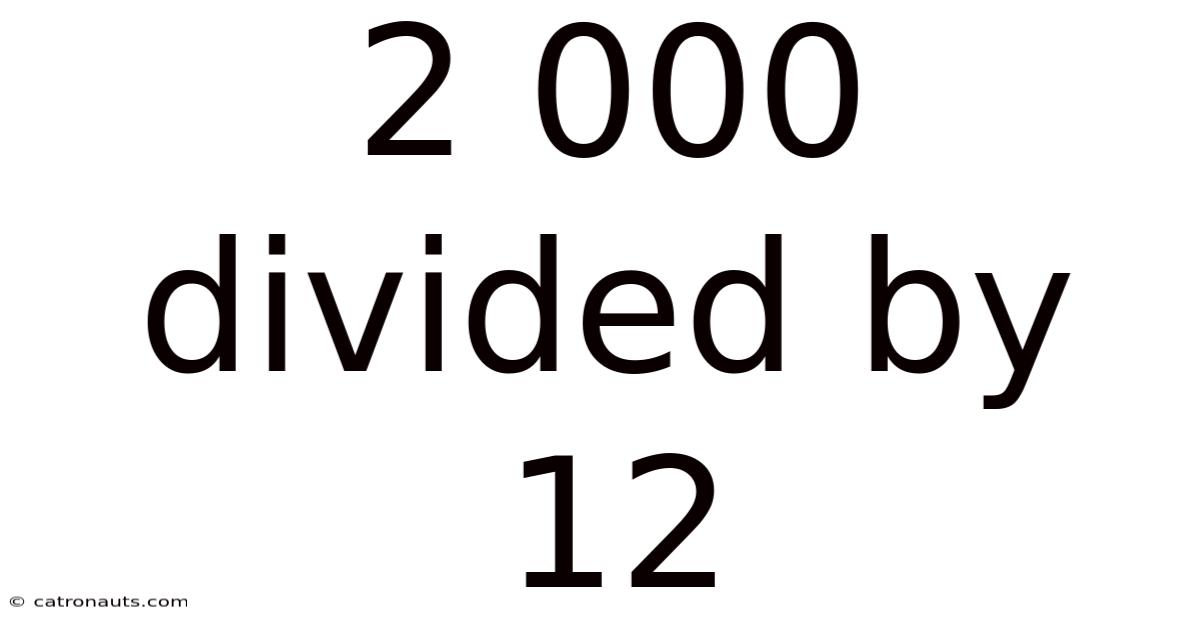
Table of Contents
Unveiling the Mystery: 2,000 Divided by 12 – A Deep Dive into Division
This article explores the seemingly simple calculation of 2,000 divided by 12, going far beyond a simple answer. We'll unpack the process, explore different methods of solving the problem, delve into the underlying mathematical principles, and even touch upon real-world applications where this type of division is crucial. Understanding this seemingly basic calculation opens doors to a deeper appreciation of arithmetic and its practical uses. Whether you're a student brushing up on your math skills or an adult looking to refresh your foundational knowledge, this comprehensive guide will equip you with a thorough understanding of division and its nuances.
Understanding the Problem: 2000 ÷ 12
The core question is: how many times does 12 go into 2000? This might seem straightforward, but understanding the process behind the answer is key to mastering division. We're not just looking for a numerical result; we're aiming to understand why that result is the answer. The problem, 2000 ÷ 12, represents the process of dividing a larger quantity (2000) into smaller, equal groups (of 12).
Methods for Solving 2000 ÷ 12
Several approaches can solve 2000 ÷ 12, each offering a unique perspective on the underlying mathematical principles.
1. Long Division: The Classic Approach
Long division is a fundamental method that systematically breaks down the division process into smaller, manageable steps. Here's how to solve 2000 ÷ 12 using long division:
-
Set up the problem: Write 2000 inside the long division symbol (⟌) and 12 outside.
-
Divide the first digits: 12 doesn't go into 2, so we consider the first two digits: 20. 12 goes into 20 one time (12 x 1 = 12). Write "1" above the 0 in 20.
-
Subtract and bring down: Subtract 12 from 20, leaving 8. Bring down the next digit, 0, to make 80.
-
Repeat the process: 12 goes into 80 six times (12 x 6 = 72). Write "6" above the 0 in 80.
-
Subtract and bring down: Subtract 72 from 80, leaving 8. Bring down the next digit, 0, to make 80.
-
Repeat again: 12 goes into 80 six times (12 x 6 = 72). Write "6" above the 0.
-
Final subtraction: Subtract 72 from 80, leaving 8. Since there are no more digits to bring down, 8 is the remainder.
Therefore, 2000 ÷ 12 = 166 with a remainder of 8. This can also be expressed as 166 8/12, which simplifies to 166 2/3.
2. Repeated Subtraction: A Conceptual Approach
Repeated subtraction offers a more intuitive understanding of division. It involves repeatedly subtracting the divisor (12) from the dividend (2000) until the remainder is less than the divisor. While less efficient for larger numbers, it helps visualize the division process:
- Subtract 12 from 2000 repeatedly until you reach a number less than 12. The number of times you subtract represents the quotient. This method is time-consuming for large numbers like 2000 but is effective for demonstrating the basic principle of division.
3. Using a Calculator: The Practical Approach
In many real-world scenarios, using a calculator provides the quickest and most efficient solution. Simply input 2000 ÷ 12 into a calculator to obtain the answer: 166.666... The calculator provides the decimal representation, which is often more useful in practical applications.
The Mathematical Explanation: Understanding Remainders and Decimals
The long division method reveals a remainder of 8. This means that after grouping the 2000 items into groups of 12, we have 8 items left over. We can express this remainder as a fraction (8/12) and simplify it to 2/3. Therefore, 2000 ÷ 12 can be represented as 166 2/3.
The decimal representation (166.666...) is an infinitely repeating decimal. This arises because the fraction 2/3 cannot be represented exactly as a terminating decimal. The repeating 6s indicate that the division continues indefinitely.
Real-World Applications: Where 2000 ÷ 12 Matters
Understanding division, especially a seemingly simple problem like 2000 ÷ 12, has numerous practical applications:
-
Resource allocation: Imagine you have 2000 apples to distribute equally among 12 baskets. The calculation helps determine how many apples go in each basket (166) and how many are left over (8).
-
Financial calculations: Dividing a total amount of money among several individuals or investments requires division. For example, splitting a $2000 profit among 12 partners involves this exact calculation.
-
Measurement and scaling: Converting units often involves division. For instance, if you need to cut a 2000-inch wire into 12 equal pieces, the calculation helps determine the length of each piece.
-
Engineering and design: In various engineering projects, calculations involving division are essential for precise measurements, resource allocation, and scaling.
Frequently Asked Questions (FAQ)
Q: Why is the decimal representation of 2000 ÷ 12 an infinitely repeating decimal?
A: The decimal representation repeats because the fraction representing the remainder (2/3) cannot be expressed exactly as a terminating decimal. The fraction 2/3 is a rational number, but its decimal equivalent is a non-terminating, repeating decimal.
Q: What is the most accurate way to represent the answer to 2000 ÷ 12?
A: The most accurate representation depends on the context. For practical purposes, the decimal approximation (166.67) might suffice. For mathematical precision, the mixed number (166 2/3) is the most accurate representation as it captures the exact value including the remainder.
Q: How can I improve my skills in division?
A: Practice is key! Start with simpler division problems and gradually increase the difficulty. Use different methods (long division, repeated subtraction) to solidify your understanding. Utilize online resources and educational materials for additional practice and guidance.
Conclusion: Beyond the Numbers
The seemingly straightforward calculation of 2000 divided by 12 offers a rich opportunity to delve into the fundamentals of division, explore various solution methods, and understand the underlying mathematical principles. From long division to repeated subtraction and calculator usage, we’ve explored multiple approaches, highlighting the versatility of this fundamental arithmetic operation. By understanding this calculation, we're not just solving a simple problem; we're building a strong foundation in mathematics, empowering ourselves to tackle more complex challenges with confidence and clarity. The real-world applications underscore the importance of mastering this seemingly simple skill, showcasing its relevance across numerous disciplines and everyday situations. Remember that consistent practice and a deeper understanding of the underlying concepts are key to mastering division and achieving mathematical proficiency.
Latest Posts
Latest Posts
-
12 25 As A Percentage
Sep 14, 2025
-
20 Out Of 30 Percentage
Sep 14, 2025
-
Advantages Of Franchisor And Franchisee
Sep 14, 2025
-
Wind In The Willows 1996
Sep 14, 2025
-
Analysis Of Sylvia Plath Daddy
Sep 14, 2025
Related Post
Thank you for visiting our website which covers about 2 000 Divided By 12 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.