20 Percent Of 400 000
catronauts
Sep 15, 2025 · 5 min read
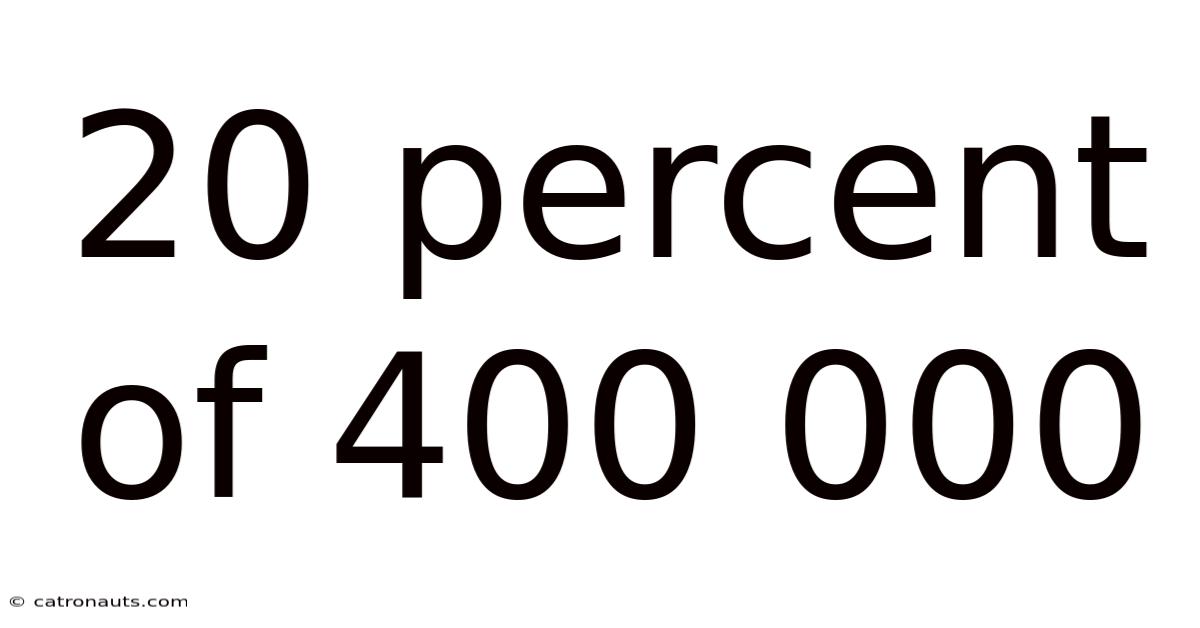
Table of Contents
Decoding 20% of 400,000: A Comprehensive Guide to Percentages
Calculating percentages is a fundamental skill in mathematics with wide-ranging applications in everyday life, from calculating discounts and sales tax to understanding financial reports and statistical data. This article dives deep into the seemingly simple calculation of 20% of 400,000, exploring various methods, explaining the underlying principles, and extending the concept to broader applications. Understanding this seemingly basic calculation can unlock a deeper comprehension of percentage-based problems.
Understanding Percentages: The Basics
Before we tackle the specific problem, let's refresh our understanding of percentages. A percentage is simply a fraction expressed as a part of 100. The symbol "%" represents "per cent," meaning "out of one hundred." Therefore, 20% can be written as 20/100, or its simplified equivalent, 1/5. This means 20% represents 20 parts out of every 100 parts.
Method 1: The Direct Calculation Method
The most straightforward approach to calculating 20% of 400,000 is to convert the percentage to a decimal and multiply it by the given number.
-
Convert the percentage to a decimal: To do this, divide the percentage by 100. 20% / 100 = 0.20 or 0.2
-
Multiply the decimal by the number: 0.2 * 400,000 = 80,000
Therefore, 20% of 400,000 is $\boxed{80,000}$.
Method 2: The Fraction Method
As mentioned earlier, 20% can be represented as the fraction 1/5. This method uses this fractional representation to solve the problem.
-
Represent the percentage as a fraction: 20% = 1/5
-
Multiply the fraction by the number: (1/5) * 400,000 = 400,000 / 5 = 80,000
This again confirms that 20% of 400,000 is $\boxed{80,000}$.
Method 3: Using Proportions
Proportions offer another effective way to solve percentage problems. This method establishes a relationship between the percentage and the whole number.
-
Set up a proportion: We can set up a proportion as follows:
x / 400,000 = 20 / 100
Where 'x' represents the value we want to find (20% of 400,000).
-
Solve for x: To solve for x, cross-multiply:
100x = 20 * 400,000
100x = 8,000,000
x = 8,000,000 / 100
x = 80,000
Once more, the result is $\boxed{80,000}$.
Why Different Methods Yield the Same Result
All three methods demonstrate different approaches to the same underlying mathematical concept. They all effectively translate the percentage into a numerical representation that can be used to calculate the required portion of the given number. The consistency in the results highlights the interconnectedness of these mathematical concepts.
Practical Applications of Percentage Calculations
Understanding percentage calculations is crucial in various real-world scenarios. Here are some examples:
-
Financial Calculations: Calculating interest on loans, determining discounts on purchases, understanding tax rates, analyzing investment returns, and calculating profit margins all involve percentage calculations.
-
Data Analysis and Statistics: Percentages are widely used to represent proportions in data analysis, such as expressing market share, survey results, and population demographics.
-
Scientific and Engineering Applications: Percentages are used in various scientific and engineering contexts, including calculating efficiency rates, expressing concentrations of substances, and representing error margins.
-
Everyday Life: We encounter percentage calculations daily, such as calculating tips at restaurants, figuring out sale prices in stores, and understanding the nutritional information on food labels.
Extending the Concept: Calculating Other Percentages of 400,000
The techniques discussed above can be applied to calculate any percentage of 400,000. For example:
-
50% of 400,000: 0.5 * 400,000 = 200,000
-
75% of 400,000: 0.75 * 400,000 = 300,000
-
15% of 400,000: 0.15 * 400,000 = 60,000
-
1% of 400,000: 0.01 * 400,000 = 4,000
Calculating Percentages with Different Numbers
The same principles apply when calculating percentages of other numbers. For example, to calculate 20% of 650,000:
-
Convert the percentage to a decimal: 20% = 0.20
-
Multiply by the number: 0.20 * 650,000 = 130,000
Therefore, 20% of 650,000 is 130,000.
Frequently Asked Questions (FAQ)
Q: What is the easiest way to calculate percentages?
A: The easiest method generally involves converting the percentage to a decimal and multiplying it by the number. This is a quick and straightforward approach suitable for most calculations.
Q: Can I use a calculator for percentage calculations?
A: Yes, calculators are extremely helpful for percentage calculations, especially for more complex problems or those involving larger numbers. Most calculators have a percentage function (%) that simplifies the process.
Q: What if the percentage is a decimal, like 2.5%?
A: Follow the same process; convert the decimal percentage (2.5% = 0.025) to a decimal and multiply it by the number.
Q: How do I calculate the percentage one number represents of another?
A: To calculate the percentage one number represents of another, divide the first number by the second number and then multiply by 100. For example, to find what percentage 80,000 is of 400,000: (80,000/400,000) * 100 = 20%.
Q: Are there any online tools or apps that can calculate percentages?
A: Yes, numerous online calculators and mobile apps are available to perform percentage calculations. These tools can be helpful for quick calculations and often provide different calculation methods.
Conclusion
Calculating 20% of 400,000, which equals 80,000, might seem like a simple calculation. However, understanding the underlying principles of percentages, the various methods to solve such problems, and the diverse applications of percentage calculations in real-world situations is essential for anyone striving for mathematical literacy and practical problem-solving skills. Mastering percentage calculations opens up a world of possibilities in personal finance, data interpretation, and countless other fields. The methods outlined in this article provide a solid foundation for tackling various percentage-related problems with confidence and accuracy. Remember, practice makes perfect; the more you work with percentages, the more comfortable and proficient you will become.
Latest Posts
Latest Posts
-
What Is Function Of Business
Sep 16, 2025
-
1 X 2 Y 2
Sep 16, 2025
-
Group Of Cattle Is Called
Sep 16, 2025
-
Holy Trinity Serbian Orthodox Church
Sep 16, 2025
-
Area Of Parallelogram In Vector
Sep 16, 2025
Related Post
Thank you for visiting our website which covers about 20 Percent Of 400 000 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.