3 4 Multiplied By 2
catronauts
Sep 12, 2025 · 6 min read
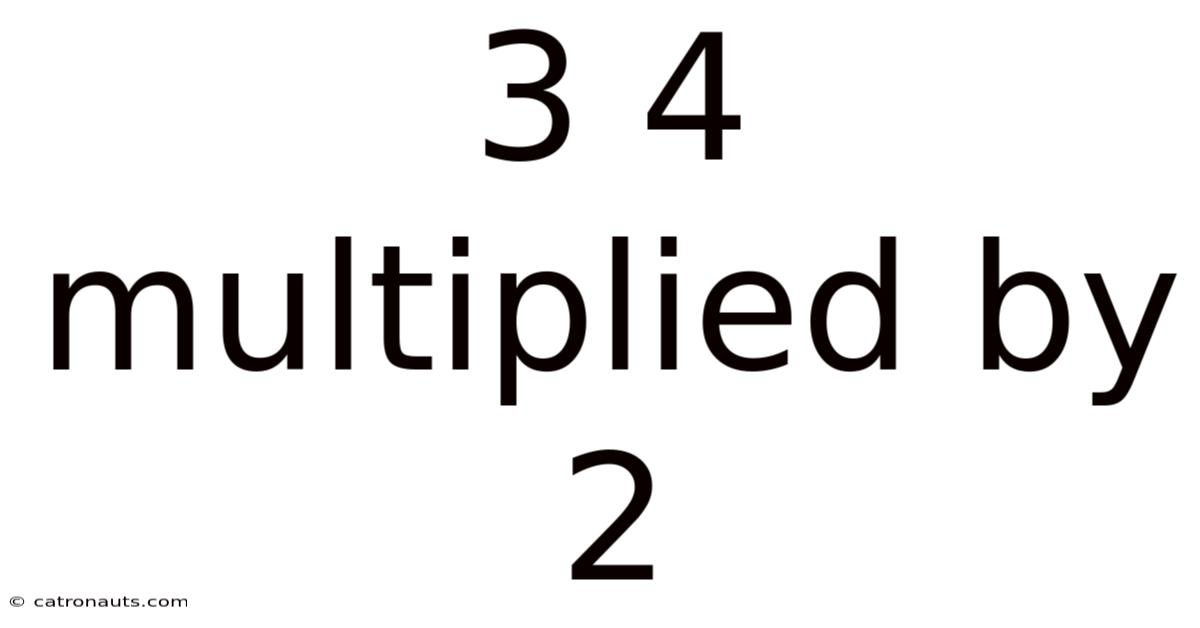
Table of Contents
Unveiling the Mystery: A Deep Dive into 34 Multiplied by 2
This article explores the seemingly simple calculation of 34 multiplied by 2, delving far beyond the basic arithmetic to uncover the underlying mathematical principles and practical applications. While the answer itself is readily obtainable (68), the journey to understanding how we arrive at that answer and the broader implications of multiplication offers invaluable insights into numerical reasoning and problem-solving. We'll unpack the process step-by-step, explore different methods of calculation, delve into the theoretical foundations, and consider real-world scenarios where this seemingly simple calculation plays a crucial role.
Introduction: The Power of Multiplication
Multiplication is a fundamental arithmetic operation representing repeated addition. It’s a cornerstone of mathematics, forming the basis for more complex calculations in algebra, calculus, and countless other fields. Understanding multiplication deeply isn’t just about getting the right answer; it's about grasping the conceptual framework that allows us to solve a wide array of problems efficiently and accurately. The seemingly simple equation, 34 x 2, provides an excellent platform to explore this foundational concept.
Step-by-Step Calculation: The Standard Method
The most common method for multiplying 34 by 2 involves using the standard algorithm. Let's break this down:
-
Multiply the units digit: We begin by multiplying the units digit of 34 (which is 4) by 2. 4 x 2 = 8. We write down '8' in the units place of our answer.
-
Multiply the tens digit: Next, we multiply the tens digit of 34 (which is 3) by 2. 3 x 2 = 6. We write down '6' in the tens place of our answer.
-
Combine the results: Combining the results from steps 1 and 2, we get 68. Therefore, 34 multiplied by 2 equals 68.
This seemingly simple process lays the foundation for understanding multiplication with larger numbers and more complex calculations.
Alternative Methods: Exploring Different Approaches
While the standard algorithm is efficient, exploring alternative methods enhances our understanding of multiplication's underlying principles. Let's consider a few:
-
Repeated Addition: This approach directly reflects the definition of multiplication as repeated addition. We can visualize 34 x 2 as adding 34 to itself: 34 + 34 = 68. This method is particularly helpful for visualizing the concept, especially for younger learners.
-
Distributive Property: The distributive property states that a(b + c) = ab + ac. We can apply this to 34 x 2 by breaking down 34 into 30 + 4:
2 x (30 + 4) = (2 x 30) + (2 x 4) = 60 + 8 = 68
This method highlights the flexibility and power of mathematical properties.
-
Using a Number Line: A number line provides a visual representation of the multiplication process. Starting at 0, we can make two jumps of 34 units each, landing at 68. This method is effective for reinforcing the concept of repeated addition.
-
Lattice Multiplication: Although less commonly used, lattice multiplication is a visually appealing and effective method, particularly useful for larger numbers. It involves creating a grid and performing smaller multiplications within the grid before summing the results diagonally.
Each of these methods, while arriving at the same answer (68), emphasizes a different aspect of the multiplication process, strengthening our understanding of its conceptual basis.
The Mathematical Foundation: Beyond the Numbers
The seemingly simple equation 34 x 2 touches upon fundamental mathematical concepts:
-
Commutative Property: Multiplication is commutative, meaning the order of the numbers doesn't affect the result. 34 x 2 is the same as 2 x 34. This property simplifies calculations and enhances our understanding of numerical relationships.
-
Associative Property: The associative property allows us to group numbers differently without changing the outcome. This is particularly relevant when multiplying more than two numbers.
-
Identity Property: Multiplying any number by 1 results in the same number. This is the identity property of multiplication. While not directly relevant to 34 x 2, it’s a crucial property in the broader context of multiplication.
-
Inverse Property: The inverse property relates to division. The inverse of multiplying by 2 is dividing by 2. Understanding this inverse relationship provides a deeper appreciation for the interconnectedness of arithmetic operations.
Real-World Applications: Where 34 x 2 Matters
While seemingly trivial, the calculation of 34 x 2 has numerous real-world applications:
-
Everyday Purchases: Imagine buying two items costing $34 each. The total cost is simply 34 x 2 = $68. This simple calculation is encountered daily in various shopping scenarios.
-
Measurement and Conversion: Suppose you're working with a length of 34 centimeters and need to find the total length of two such pieces. The calculation 34 x 2 = 68 centimeters provides the answer. Similar applications exist across various units of measurement.
-
Inventory Management: In a warehouse, if there are 34 boxes of a particular item and you need to double the stock, you'll need 34 x 2 = 68 boxes.
-
Construction and Engineering: Numerous calculations in construction and engineering involve simple multiplications, with 34 x 2 being a potential component in larger, more complex calculations.
-
Data Analysis: While often involving larger numbers, basic multiplication forms the foundation of many data analysis techniques. Understanding simple multiplications like 34 x 2 is crucial for building a solid foundation in data analysis.
These examples illustrate that the seemingly simple calculation 34 x 2 isn't just an abstract mathematical exercise; it's a practical tool used across various fields.
Extending the Concept: Beyond 34 x 2
Understanding 34 x 2 provides a solid foundation for tackling more complex multiplication problems. The principles discussed here – the standard algorithm, alternative methods, and underlying mathematical properties – are directly applicable to larger numbers and more complex equations. By mastering the fundamentals, you’ll be well-equipped to handle more advanced mathematical challenges. Consider applying these principles to problems such as 123 x 4, 567 x 8, or even larger multiplications.
Frequently Asked Questions (FAQ)
-
Q: What is the easiest way to calculate 34 x 2?
A: The easiest method depends on individual preference and understanding. The standard algorithm is efficient, while repeated addition provides a visual understanding. The distributive property offers a flexible approach.
-
Q: Why is understanding multiplication important?
A: Multiplication is fundamental to mathematics and its applications. It forms the basis for more complex calculations and is essential in various fields, from everyday shopping to advanced engineering.
-
Q: Can I use a calculator for 34 x 2?
A: While a calculator provides a quick answer, understanding the underlying process is crucial for developing mathematical reasoning and problem-solving skills.
Conclusion: The Enduring Value of Simple Arithmetic
The seemingly simple calculation of 34 multiplied by 2 offers a rich opportunity to explore fundamental mathematical principles and their practical applications. By understanding the various methods of calculation, the underlying mathematical properties, and the diverse real-world applications, we not only find the answer (68) but also gain a deeper appreciation for the power and elegance of mathematics. This journey extends far beyond a simple arithmetic problem; it's a stepping stone toward a deeper understanding of numerical reasoning and its importance in our world. The key takeaway isn't just the answer itself, but the broader understanding of mathematical concepts and their practical relevance that it unlocks.
Latest Posts
Latest Posts
-
Words That Have 2 Meanings
Sep 12, 2025
-
3 Out Of 8 Percentage
Sep 12, 2025
-
How Did Willem Janszoon Die
Sep 12, 2025
-
Paintings Of The 19th Century
Sep 12, 2025
-
What Is Deposition In Science
Sep 12, 2025
Related Post
Thank you for visiting our website which covers about 3 4 Multiplied By 2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.