3 Out Of 8 Percentage
catronauts
Sep 12, 2025 · 5 min read
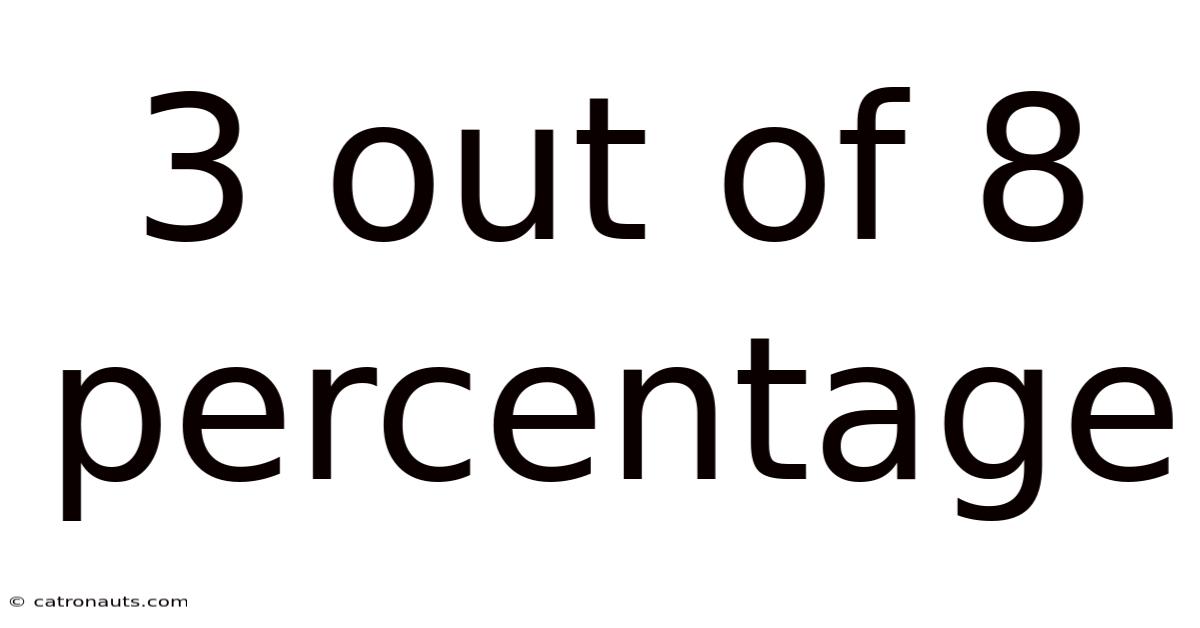
Table of Contents
Understanding 3 out of 8: Percentages, Fractions, and Real-World Applications
Calculating percentages is a fundamental skill applicable across various aspects of life, from understanding sales discounts to analyzing statistical data. This article delves into the seemingly simple calculation of "3 out of 8," explaining its representation as a fraction, a decimal, and a percentage, and then exploring its broader implications within different contexts. We'll move beyond the basic calculation to explore how this concept relates to probability, statistics, and real-world scenarios. This comprehensive guide will equip you with the knowledge and understanding to confidently tackle similar percentage problems in the future.
From Fraction to Percentage: Breaking Down 3 out of 8
The phrase "3 out of 8" immediately suggests a fraction: 3/8. This fraction represents a part of a whole, where 3 is the part and 8 is the whole. To convert this fraction into a percentage, we need to understand that a percentage is simply a fraction expressed as a part of 100.
Step-by-step conversion:
-
Divide the numerator by the denominator: Divide 3 by 8: 3 ÷ 8 = 0.375
-
Multiply by 100: Multiply the decimal result by 100 to express it as a percentage: 0.375 x 100 = 37.5
-
Add the percentage symbol: The final result is 37.5%.
Therefore, 3 out of 8 is equal to 37.5%.
Visualizing the Percentage: Understanding Proportions
Visualizing percentages can significantly improve comprehension. Imagine a pie chart divided into 8 equal slices. If 3 of these slices are shaded, the shaded area represents 37.5% of the whole pie. This visual representation helps to understand the proportional relationship between the part (3 slices) and the whole (8 slices). Similar visual aids, such as bar graphs or number lines, can be used to illustrate the concept effectively.
Practical Applications of 37.5%
The concept of "3 out of 8," or 37.5%, appears in many everyday situations:
- Sales and Discounts: A store might offer a 37.5% discount on selected items.
- Test Scores: A student might achieve a score of 3 out of 8 questions correct on a quiz.
- Survey Results: In a survey of 8 people, 3 might have responded positively to a particular question.
- Statistical Analysis: In a sample of 8 observations, 3 might possess a specific characteristic.
- Probability: In a situation with 8 equally likely outcomes, the probability of a specific event occurring 3 times is related to this percentage.
Beyond the Basics: Exploring Probability and Statistics
The concept of 3 out of 8 extends beyond simple percentage calculations and has significant implications in probability and statistics.
Probability: If we consider a scenario with 8 equally likely outcomes, the probability of a specific event occurring 3 times out of 8 trials can be calculated using various probability distributions, depending on whether the trials are independent or dependent. For independent trials, the binomial distribution would be appropriate. The calculation involves combinations and probabilities for each individual trial.
Statistics: In statistical analysis, "3 out of 8" might represent a sample proportion. This sample proportion could be used to estimate the population proportion. However, it's crucial to remember that a sample proportion is only an estimate, and its accuracy depends on the sample size. Larger sample sizes generally lead to more reliable estimates. Inferential statistics uses sample data to make inferences about a larger population. The concept of sampling error and confidence intervals become important when dealing with such sample proportions. Understanding the margin of error associated with the sample would give a more accurate representation of the true population percentage.
Addressing Common Misconceptions
Several misconceptions can arise when working with percentages:
-
Confusing percentages with fractions: While percentages and fractions are closely related, they are not interchangeable in all contexts. A percentage is always a fraction expressed out of 100, while a fraction can represent any part of a whole.
-
Incorrectly calculating percentages: Common errors include incorrect division, multiplication, or forgetting to multiply by 100 when converting a decimal to a percentage.
-
Misinterpreting percentage increases and decreases: A 10% increase followed by a 10% decrease does not result in the original value; this is due to the different bases for the percentage calculations.
-
Ignoring the context: The meaning of a percentage depends heavily on the context. A 37.5% success rate in one context might be considered excellent, while in another, it might be considered poor.
Frequently Asked Questions (FAQs)
Q: How do I calculate a percentage increase or decrease from a base value?
A: To calculate a percentage increase, find the difference between the new value and the base value, divide the difference by the base value, and multiply by 100. To calculate a percentage decrease, follow the same process, but the result will be negative.
Q: What is the difference between a relative and an absolute percentage change?
A: An absolute percentage change refers to the simple percentage difference between two values. A relative percentage change considers the context or base value more significantly. For example, a 10% increase from 100 to 110 is an absolute 10% change. But a 10% increase from 10 to 11 might be less significant in certain applications.
Q: Can I use a calculator to calculate percentages?
A: Yes, most calculators have a percentage function that simplifies the calculation process. Many online calculators are also available.
Q: How do I convert a decimal to a percentage?
A: Multiply the decimal by 100 and add the percentage symbol (%).
Q: How can I improve my understanding of percentages?
A: Practice regularly with different examples and try to visualize the percentages using diagrams. Focus on understanding the underlying principles rather than just memorizing formulas.
Conclusion: Mastering Percentages for Real-World Success
Understanding percentages is a crucial skill for navigating various aspects of daily life and professional endeavors. This article has explored the calculation and application of "3 out of 8" as a percentage (37.5%), extending the discussion to include probability, statistics, and common misconceptions. By grasping the fundamental principles and applying the techniques outlined here, you will be well-equipped to confidently tackle percentage-related problems and make informed decisions based on quantitative data. Remember that the key to mastering percentages lies in consistent practice and a thorough understanding of the underlying concepts. Don't hesitate to review the steps and examples provided to solidify your understanding and build your confidence in handling percentages effectively. With practice, these calculations will become second nature.
Latest Posts
Latest Posts
-
Parts Of A Corn Plant
Sep 12, 2025
-
18 60 As A Percentage
Sep 12, 2025
-
Example Of Conclusion In Science
Sep 12, 2025
-
Age Of Consent In Mississippi
Sep 12, 2025
-
Because Of Winn Dixie Narrator
Sep 12, 2025
Related Post
Thank you for visiting our website which covers about 3 Out Of 8 Percentage . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.