3 5 As A Percent
catronauts
Sep 12, 2025 · 6 min read
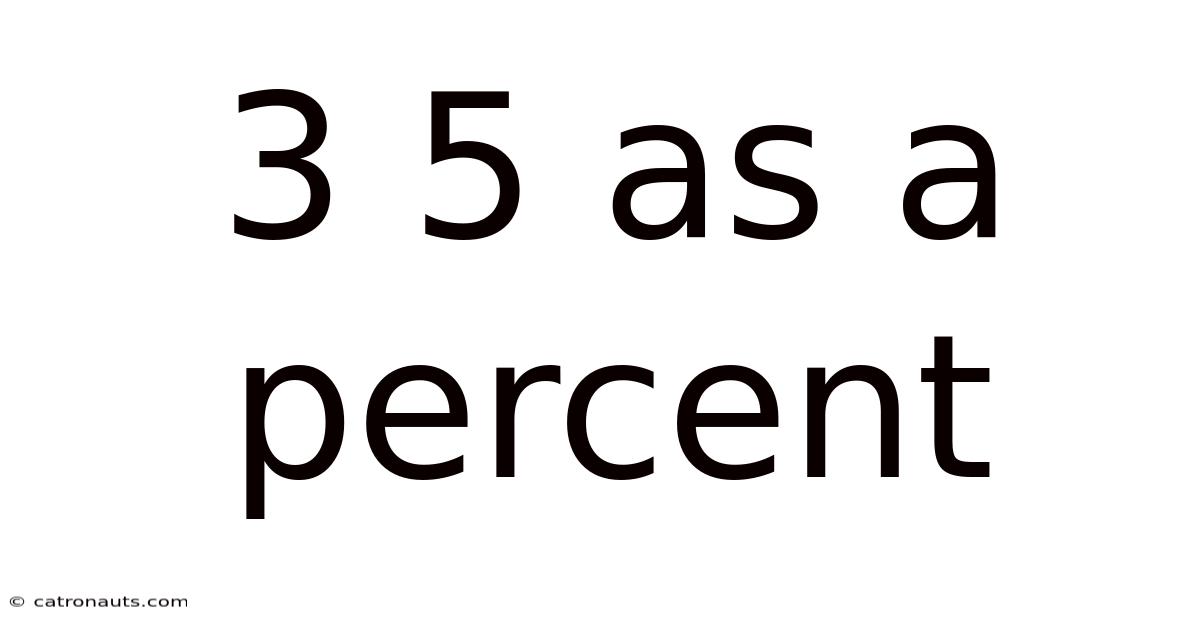
Table of Contents
3/5 as a Percent: A Comprehensive Guide
Understanding fractions and their percentage equivalents is a fundamental skill in mathematics with wide-ranging applications in everyday life, from calculating discounts and tips to understanding financial reports and analyzing data. This comprehensive guide will explore how to convert the fraction 3/5 into a percentage, explaining the process in detail and providing additional context to solidify your understanding. We'll cover the core conversion method, explore different approaches, address common misconceptions, and delve into the practical applications of this conversion.
Understanding Fractions and Percentages
Before diving into the conversion of 3/5 to a percentage, let's briefly review the concepts of fractions and percentages.
-
Fractions: A fraction represents a part of a whole. It consists of two numbers: the numerator (the top number) and the denominator (the bottom number). The numerator indicates how many parts you have, while the denominator indicates the total number of equal parts the whole is divided into. For example, in the fraction 3/5, 3 is the numerator and 5 is the denominator. This means we have 3 parts out of a total of 5 equal parts.
-
Percentages: A percentage is a way of expressing a fraction or a decimal as a proportion of 100. The term "percent" literally means "out of 100" (per centum in Latin). Percentages are often used to represent proportions, rates, or changes in quantities. For instance, 50% means 50 out of 100, or 50/100, which simplifies to 1/2.
Converting 3/5 to a Percentage: The Primary Method
The most straightforward method to convert 3/5 to a percentage involves two simple steps:
Step 1: Convert the fraction to a decimal. To do this, divide the numerator (3) by the denominator (5):
3 ÷ 5 = 0.6
Step 2: Convert the decimal to a percentage. Multiply the decimal by 100 and add the percentage symbol (%):
0.6 x 100 = 60%
Therefore, 3/5 is equal to 60%.
Alternative Methods for Conversion
While the above method is the most common and arguably the easiest, there are alternative approaches that can be useful depending on your preference or the specific context:
Method 1: Using Equivalent Fractions
You can convert the fraction 3/5 into an equivalent fraction with a denominator of 100. Since percentages are based on 100, this method directly yields the percentage value. To find an equivalent fraction with a denominator of 100, we need to determine what number we multiply 5 by to get 100. This is 20 (100 ÷ 5 = 20). We must then multiply both the numerator and the denominator by 20 to maintain the proportional value:
(3 x 20) / (5 x 20) = 60/100
Since 60/100 means 60 out of 100, this is equivalent to 60%.
Method 2: Using Proportions
We can also solve this using proportions. We can set up a proportion where x represents the percentage we're looking for:
3/5 = x/100
To solve for x, we cross-multiply:
5x = 300
x = 300 ÷ 5
x = 60
Therefore, 3/5 is equal to 60%.
Understanding the Significance of 60%
60% represents a significant proportion. It's more than half (50%) but less than the whole (100%). Understanding its context is crucial. For example, if you scored 3 out of 5 on a quiz, you achieved a 60% score. In a business context, a 60% market share indicates a strong position within the industry. The interpretation of 60% varies depending on the specific application.
Common Misconceptions and Pitfalls
While converting fractions to percentages is a relatively straightforward process, some common misconceptions can lead to errors:
-
Incorrect Decimal Placement: A common mistake is incorrectly placing the decimal point when converting a decimal to a percentage. Remember to multiply by 100, which effectively moves the decimal point two places to the right.
-
Forgetting the Percentage Symbol: Always remember to add the percentage symbol (%) after converting to a percentage. This is crucial for clear communication and to avoid ambiguity.
-
Confusing Numerator and Denominator: Ensure you divide the numerator by the denominator correctly. Dividing the denominator by the numerator will yield an incorrect result.
Practical Applications of 3/5 and 60%
The ability to convert fractions like 3/5 to percentages is essential in numerous real-world situations:
-
Calculating Grades: As mentioned earlier, converting a fraction score (e.g., 3 correct answers out of 5 questions) to a percentage grade (60%) is a common application.
-
Understanding Discounts: Sales often advertise discounts as percentages. If an item is discounted by 60%, you can easily calculate the final price.
-
Analyzing Data: In statistics and data analysis, percentages are frequently used to represent proportions and trends within data sets. Understanding how to convert fractions to percentages is essential for interpreting this data effectively.
-
Financial Calculations: Percentages are fundamental in finance, used in calculations related to interest rates, taxes, profits, and losses. The ability to convert fractions to percentages is critical for understanding and managing finances.
-
Everyday Life: From calculating tips in restaurants to understanding sales tax, percentages are pervasive in our daily lives.
Frequently Asked Questions (FAQ)
-
Q: Can I convert any fraction to a percentage? A: Yes, you can convert any fraction to a percentage by following the methods outlined above.
-
Q: What if the decimal has more than two places after the decimal point? A: Simply multiply the decimal by 100, and round to the desired number of decimal places in the percentage.
-
Q: Is there a formula for converting fractions to percentages? A: Essentially, the formula is: (Numerator / Denominator) * 100 = Percentage
-
Q: Why are percentages useful? A: Percentages provide a standardized way to compare proportions and make calculations easier than working directly with fractions or decimals.
-
Q: Are there any online calculators that can help with this conversion? A: Many online calculators are available to help convert fractions to percentages. However, understanding the underlying process is far more beneficial in the long run.
Conclusion
Converting 3/5 to a percentage, resulting in 60%, is a simple yet crucial mathematical operation. Mastering this skill unlocks a deeper understanding of fractional and percentage representations and expands your ability to solve practical problems in various fields. By understanding the different methods, common pitfalls, and the numerous applications of this conversion, you'll be well-equipped to confidently tackle percentage-related calculations in your daily life and academic or professional pursuits. Remember to practice regularly to solidify your understanding and build proficiency in working with fractions and percentages. The more you practice, the easier and more intuitive these concepts will become. This comprehensive understanding will undoubtedly prove invaluable as you continue your mathematical journey.
Latest Posts
Latest Posts
-
Compound Interest Formula In Excel
Sep 12, 2025
-
What Is Net Realizable Value
Sep 12, 2025
-
Is Wrist Distal To Elbow
Sep 12, 2025
-
Lewis Dot Structure For Chcl3
Sep 12, 2025
-
Difference Between Transparent And Translucent
Sep 12, 2025
Related Post
Thank you for visiting our website which covers about 3 5 As A Percent . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.