Factor X 2 X 2
catronauts
Sep 16, 2025 · 5 min read
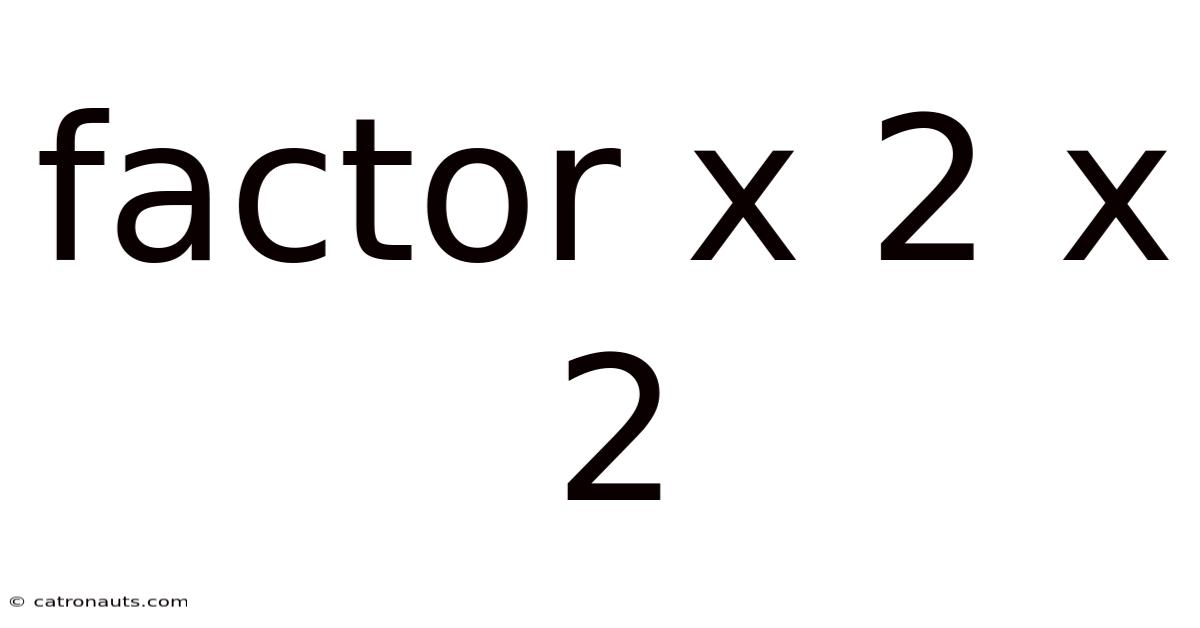
Table of Contents
Decoding the Enigma: A Deep Dive into Factorial 2 x 2
The seemingly simple expression "factorial 2 x 2" often leads to confusion, especially for those new to mathematical notation. This article will delve into the meaning of this expression, providing a comprehensive explanation suitable for both beginners and those seeking a more thorough understanding. We'll unravel the concepts of factorials, multiplication, and the order of operations, ensuring a clear and complete comprehension. By the end, you'll not only know the answer but also grasp the underlying mathematical principles.
Understanding Factorials: The Basics
Before tackling "factorial 2 x 2," let's define the core concept: the factorial. A factorial, denoted by an exclamation mark (!), represents the product of all positive integers less than or equal to a given number. For instance:
- 1! = 1 (One factorial is one)
- 2! = 2 x 1 = 2 (Two factorial is two multiplied by one)
- 3! = 3 x 2 x 1 = 6 (Three factorial is three multiplied by two multiplied by one)
- 4! = 4 x 3 x 2 x 1 = 24 (Four factorial is four multiplied by three multiplied by two multiplied by one), and so on.
In essence, the factorial of a number n (denoted as n!) is calculated as n x (n-1) x (n-2) x ... x 2 x 1. Factorials are crucial in various areas of mathematics, including combinatorics (counting arrangements) and probability calculations. They represent the number of ways to arrange a set of objects. For example, 3! = 6 represents the six possible ways to arrange three distinct objects.
Deconstructing "Factorial 2 x 2"
Now, let's analyze the expression "factorial 2 x 2." The key is to understand the order of operations, often remembered by the acronym PEMDAS/BODMAS (Parentheses/Brackets, Exponents/Orders, Multiplication and Division, Addition and Subtraction). In this case, we have a factorial and multiplication. Factorials take precedence over multiplication. Therefore, we calculate the factorial first.
The expression breaks down as follows:
-
Calculate the factorial: The expression includes "factorial 2," which is written as 2!. As we established earlier, 2! = 2 x 1 = 2.
-
Perform the multiplication: After calculating the factorial, we are left with 2 x 2. This is a simple multiplication problem: 2 x 2 = 4.
Therefore, the solution to "factorial 2 x 2" is 4.
Beyond the Basics: Extending the Concept
While "factorial 2 x 2" is a relatively simple example, understanding factorials extends to more complex scenarios. Let's explore some related concepts and expand our understanding:
-
Factorials of Larger Numbers: As mentioned earlier, factorials quickly increase in value. For instance, 5! = 120, 10! = 3,628,800, and so on. Calculating factorials for large numbers often requires computational tools.
-
Factorials and Combinations: Factorials play a pivotal role in calculating combinations. A combination is a selection of items from a larger set, where the order of selection doesn't matter. The formula for combinations involves factorials:
nCr = n! / (r! * (n-r)!)
Where:
- n is the total number of items.
- r is the number of items to be selected.
- nCr represents the number of combinations.
-
Factorials and Permutations: Similar to combinations, permutations involve selecting items from a set, but the order of selection does matter. The formula for permutations also utilizes factorials:
nPr = n! / (n-r)!
Where:
- n is the total number of items.
- r is the number of items to be selected.
- nPr represents the number of permutations.
-
The Gamma Function: For non-integer values, the factorial is generalized using the Gamma function, a more complex mathematical function that extends the concept of factorials to complex numbers. This is a significant topic in advanced mathematics and beyond the scope of this introductory article.
Applications of Factorials in Real-World Scenarios
Factorials are not merely abstract mathematical concepts; they have numerous practical applications. Here are some examples:
-
Probability and Statistics: Factorials are essential in probability calculations, especially when dealing with permutations and combinations. Determining the likelihood of specific events often requires factorial calculations.
-
Cryptography: Factorials are employed in some cryptographic algorithms, contributing to the security of encrypted data.
-
Computer Science: In computer science, factorials are used in algorithm analysis to determine the complexity of sorting and searching algorithms.
-
Physics and Engineering: Factorials appear in various physical and engineering formulas, particularly in statistical mechanics and quantum physics.
Frequently Asked Questions (FAQ)
Q: What happens if I try to calculate the factorial of a negative number?
A: The factorial function is not defined for negative numbers. Factorials are only defined for non-negative integers (0, 1, 2, 3,...).
Q: Is there a limit to how large a factorial I can calculate?
A: While theoretically you can calculate the factorial of any non-negative integer, in practice, there are limitations due to computational constraints. Very large factorials can exceed the capacity of even the most powerful computers.
Q: How do I calculate factorials on a calculator or computer?
A: Most scientific calculators and computer programming languages (like Python, R, etc.) have built-in functions to compute factorials. For instance, in Python, you would use the math.factorial() function.
Q: What if the expression was (2!) x 2? Would the answer be different?
A: No, the answer would still be 4. The parentheses simply clarify the order of operations, emphasizing that the factorial should be calculated first. However, even without the parentheses, the standard order of operations would dictate that the factorial is computed before the multiplication.
Q: Can factorials be used with decimal numbers?
A: Not directly. The standard factorial function only applies to non-negative integers. However, the Gamma function extends the concept to include non-integer values.
Conclusion: Mastering the Factorial
Understanding the concept of factorials is crucial for grasping many mathematical and scientific principles. While the expression "factorial 2 x 2" might seem simple, it serves as a gateway to comprehending the broader significance of factorials in various fields. Remember the order of operations and the definition of factorials, and you'll be well-equipped to tackle more complex calculations involving this fundamental mathematical function. This deep dive into factorial calculations, beyond the simple solution of 4, provides a robust foundation for further exploration into combinatorics, probability, and advanced mathematical concepts. The seemingly simple "factorial 2 x 2" unlocks a world of possibilities in mathematical understanding.
Latest Posts
Latest Posts
-
What Is Function Of Business
Sep 16, 2025
-
1 X 2 Y 2
Sep 16, 2025
-
Group Of Cattle Is Called
Sep 16, 2025
-
Holy Trinity Serbian Orthodox Church
Sep 16, 2025
-
Area Of Parallelogram In Vector
Sep 16, 2025
Related Post
Thank you for visiting our website which covers about Factor X 2 X 2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.