What Is 5 Of 20
catronauts
Sep 14, 2025 · 6 min read
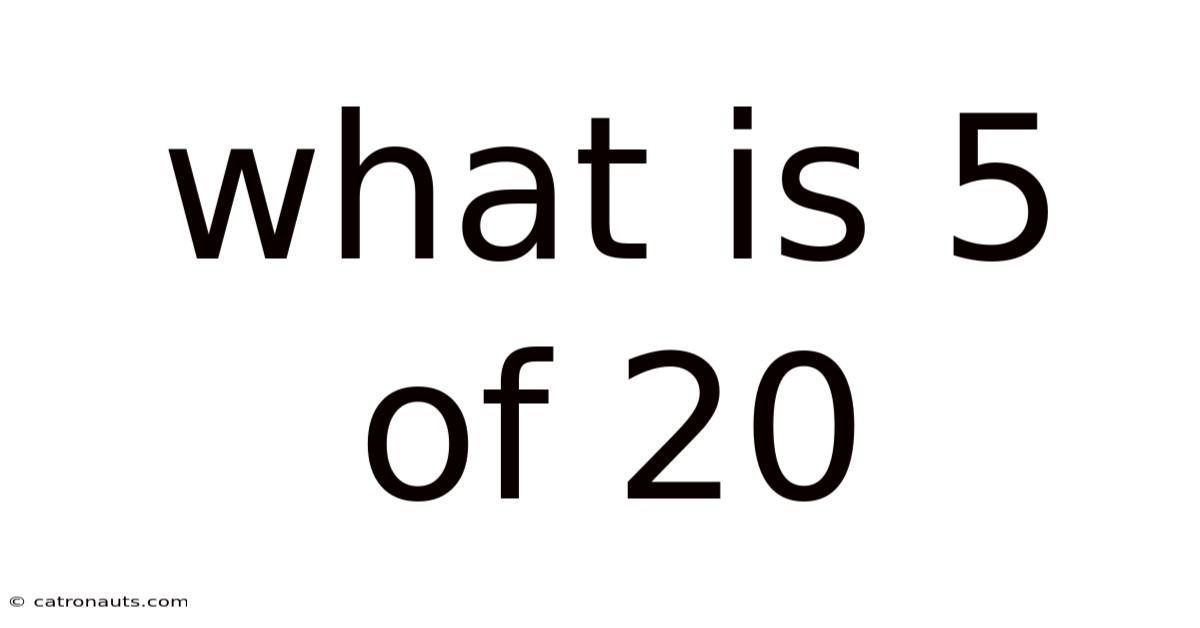
Table of Contents
What is 5 of 20? Understanding Fractions, Ratios, and Percentages
This article explores the seemingly simple question, "What is 5 of 20?" While the answer might appear immediately obvious to some, delving deeper reveals a rich tapestry of mathematical concepts, including fractions, ratios, and percentages. Understanding these concepts is crucial for various aspects of life, from everyday budgeting to advanced scientific calculations. We'll break down the answer and explore the underlying mathematical principles in a clear and accessible way.
Understanding the Fundamentals: Fractions, Ratios, and Percentages
Before we tackle "5 of 20," let's establish a solid foundation in the three key mathematical concepts that will help us understand this problem fully:
-
Fractions: A fraction represents a part of a whole. It's written as a ratio of two numbers, the numerator (top number) and the denominator (bottom number). The denominator indicates the total number of parts, while the numerator indicates the number of parts we're considering. For example, 1/2 (one-half) means one part out of two equal parts.
-
Ratios: A ratio compares two or more quantities. It shows the relative sizes of the quantities. Ratios can be expressed in several ways: using the colon (e.g., 5:20), using the word "to" (e.g., 5 to 20), or as a fraction (e.g., 5/20).
-
Percentages: A percentage represents a fraction of 100. It expresses a proportion as a number out of 100. The symbol "%" is used to denote a percentage. For example, 50% means 50 out of 100, or 50/100, which simplifies to 1/2.
What is 5 of 20? A Step-by-Step Approach
Now, let's tackle the question: "What is 5 of 20?" This phrase can be interpreted in several ways, all leading to the same core mathematical operation.
1. The Fraction Approach:
"5 of 20" can be directly translated into a fraction: 5/20. This means 5 parts out of a total of 20 parts. This fraction can be simplified by finding the greatest common divisor (GCD) of 5 and 20, which is 5. Dividing both the numerator and the denominator by 5 gives us:
5/20 = 1/4
Therefore, 5 of 20 is equivalent to one-quarter (1/4).
2. The Ratio Approach:
We can express the relationship between 5 and 20 as a ratio: 5:20. This ratio simplifies to 1:4, showing that for every one part, there are four parts in total. This confirms our fraction result: 5 out of 20 is the same as 1 out of 4.
3. The Percentage Approach:
To express 5 out of 20 as a percentage, we can set up a proportion:
5/20 = x/100
To solve for x (the percentage), we can cross-multiply:
20x = 500
x = 500/20
x = 25
Therefore, 5 of 20 is equivalent to 25%. This means that 5 represents 25% of the total of 20.
Real-World Applications: Understanding Proportions
Understanding fractions, ratios, and percentages, as demonstrated through the example of "5 of 20," is vital in many real-world scenarios. Here are a few examples:
-
Baking: A recipe calls for 20 ounces of flour, and you only want to make a quarter of the recipe. Using the fraction 1/4 (which we established is equivalent to 5/20), you would use 5 ounces of flour.
-
Shopping: A store offers a 25% discount on an item originally priced at $20. Using our percentage calculation, the discount amounts to $5 (25% of $20), meaning the final price is $15.
-
Probability: If there are 20 marbles in a bag, 5 of which are red, the probability of picking a red marble at random is 5/20, or 1/4 (25%).
-
Data Analysis: Imagine you're analyzing survey results. If 20 people participated, and 5 responded positively to a particular question, you can represent this as a fraction (5/20), a ratio (5:20), or a percentage (25%).
Expanding Our Understanding: Proportions and Problem Solving
The concept of "5 of 20" can be extended to more complex problems involving proportions. Let's consider a scenario:
-
Problem: A farmer has 20 sheep. If 5 of them are pregnant, what percentage of the sheep are pregnant?
-
Solution: This problem uses the same fundamental principles we've discussed. The fraction representing pregnant sheep is 5/20, which simplifies to 1/4 or 25%. Therefore, 25% of the farmer's sheep are pregnant.
This exemplifies how a seemingly simple question like "5 of 20" forms the basis for solving more complex real-world problems involving proportions.
Beyond the Basics: Working with Larger Numbers and Decimals
The principles we've discussed remain the same even when dealing with larger numbers or decimals. For instance, consider the question: "What is 15 of 60?"
-
Fraction: 15/60 simplifies to 1/4 (or 0.25).
-
Ratio: 15:60 simplifies to 1:4.
-
Percentage: 15/60 * 100 = 25%
This shows the consistent application of the core concepts regardless of the specific numbers involved. The ability to simplify fractions and ratios is key to efficient problem-solving.
Frequently Asked Questions (FAQ)
-
Q: Is there only one way to represent "5 of 20"?
A: No, as we've seen, "5 of 20" can be expressed as a fraction (5/20, 1/4), a ratio (5:20, 1:4), or a percentage (25%). The best representation depends on the context of the problem.
-
Q: Why is simplifying fractions important?
A: Simplifying fractions makes it easier to understand the relationship between the parts and the whole. It also makes calculations simpler and more efficient.
-
Q: How can I improve my understanding of fractions, ratios, and percentages?
A: Practice is key! Work through various problems, starting with simple ones and gradually increasing the complexity. There are many online resources and workbooks available to help you practice.
-
Q: What if the numbers aren't whole numbers?
A: The principles remain the same. You can use the same methods to express the relationship between any two numbers, whether they are whole numbers, decimals, or fractions.
Conclusion: The Power of Understanding Proportions
The seemingly simple question, "What is 5 of 20?", opens a door to a world of mathematical concepts and their practical applications. By understanding fractions, ratios, and percentages, and by mastering the ability to simplify and convert between these representations, you equip yourself with essential tools for tackling a wide range of mathematical problems and real-world situations. From baking to budgeting, from probability to data analysis, the ability to understand and manipulate proportions is a skill that will serve you well throughout your life. Remember, the key is to understand the underlying principles and to practice applying them regularly. With practice, you'll develop confidence and fluency in working with proportions, making them an intuitive and valuable part of your mathematical toolkit.
Latest Posts
Latest Posts
-
What Is Anionic And Cationic
Sep 15, 2025
-
Legal Consent Age In Mississippi
Sep 15, 2025
-
Was Muscovy A Mongol Subject
Sep 15, 2025
-
Anthem For Doomed Youth Paraphrase
Sep 15, 2025
-
3 4 Cups Times 4
Sep 15, 2025
Related Post
Thank you for visiting our website which covers about What Is 5 Of 20 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.