What's 1.2 As A Fraction
catronauts
Sep 17, 2025 · 5 min read
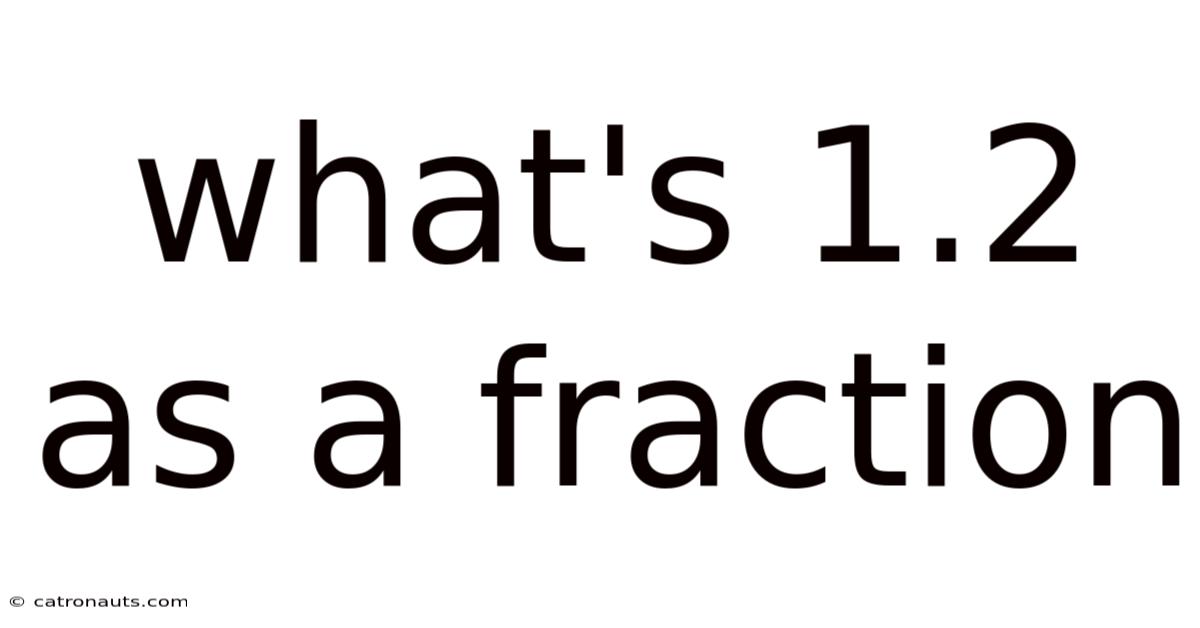
Table of Contents
What's 1.2 as a Fraction? A Comprehensive Guide
Decimals and fractions are two sides of the same coin, representing parts of a whole. Understanding how to convert between them is a fundamental skill in mathematics. This article provides a comprehensive guide to converting the decimal 1.2 into a fraction, explaining the process step-by-step and exploring the underlying mathematical principles. We'll cover various methods, address common misconceptions, and even delve into the broader context of decimal-fraction conversion. By the end, you'll not only know that 1.2 is equal to 6/5 but also possess a deeper understanding of the relationship between decimals and fractions.
Understanding Decimals and Fractions
Before diving into the conversion, let's refresh our understanding of decimals and fractions. A decimal is a number expressed in the base-ten numeral system, using a decimal point to separate the integer part from the fractional part. For instance, in 1.2, the '1' represents one whole unit, and the '.2' represents two-tenths of a unit.
A fraction, on the other hand, represents a part of a whole using a numerator (the top number) and a denominator (the bottom number). The numerator indicates how many parts we have, and the denominator indicates how many equal parts the whole is divided into. For example, in the fraction 1/2, the numerator is 1, and the denominator is 2, meaning we have one out of two equal parts.
Converting 1.2 to a Fraction: Step-by-Step Guide
The conversion of 1.2 to a fraction is relatively straightforward. Here's the process:
Step 1: Write the decimal as a fraction over 1.
This is the first step in converting any decimal to a fraction. We can write 1.2 as:
1.2/1
Step 2: Multiply the numerator and denominator by a power of 10 to eliminate the decimal point.
The decimal 1.2 has one digit after the decimal point. To eliminate this, we multiply both the numerator and the denominator by 10 (10 to the power of 1, as there is one digit after the decimal point). This gives us:
(1.2 x 10) / (1 x 10) = 12/10
Step 3: Simplify the fraction.
The fraction 12/10 can be simplified by finding the greatest common divisor (GCD) of the numerator and denominator. The GCD of 12 and 10 is 2. We divide both the numerator and the denominator by 2:
12/2 = 6 10/2 = 5
Therefore, the simplified fraction is 6/5.
Therefore, 1.2 as a fraction is 6/5.
Understanding the Result: 6/5 – An Improper Fraction
Notice that 6/5 is an improper fraction, meaning the numerator (6) is larger than the denominator (5). This reflects the fact that 1.2 is greater than 1. We can convert this improper fraction into a mixed number, which combines a whole number and a proper fraction.
To convert 6/5 to a mixed number, we divide the numerator (6) by the denominator (5):
6 ÷ 5 = 1 with a remainder of 1.
This means that 6/5 is equal to 1 and 1/5. So, 1.2 can also be represented as the mixed number 1 1/5.
Alternative Methods for Conversion
While the method above is the most common, there are other ways to convert 1.2 to a fraction:
-
Directly writing the fractional part: We can directly interpret the decimal part. The '.2' represents two-tenths, which can be written as 2/10. Adding the whole number part (1), we get 1 + 2/10. Simplifying 2/10 to 1/5, we get 1 1/5, which is equivalent to 6/5.
-
Using percentage: We can express 1.2 as a percentage (120%). Then, we can convert the percentage to a fraction by dividing by 100. 120/100 simplifies to 6/5. This method highlights the connection between decimals, percentages, and fractions.
Explaining the Mathematics: Place Value and Fractions
The conversion process relies heavily on the concept of place value. In the decimal 1.2, the '2' is in the tenths place, meaning it represents 2/10. Multiplying by 10 shifts the digit to the ones place, effectively removing the decimal point and converting the decimal part into a whole number. This is the core logic behind the multiplication step in our main conversion method.
Frequently Asked Questions (FAQ)
Q: Can all decimals be converted to fractions?
A: Yes, all terminating and repeating decimals can be converted to fractions. Terminating decimals have a finite number of digits after the decimal point (like 1.2), while repeating decimals have a pattern of digits that repeats infinitely (like 0.333...). Non-repeating, non-terminating decimals (like π) cannot be expressed as fractions.
Q: Why do we simplify fractions?
A: Simplifying fractions makes them easier to understand and work with. A simplified fraction represents the same value as the original fraction but in its most concise form.
Q: What if the decimal had more digits after the decimal point?
A: The process remains the same. If you had a decimal like 1.234, you would multiply the numerator and denominator by 1000 (10 to the power of 3, as there are three digits after the decimal point) to remove the decimal point.
Q: Is there a difference between 6/5 and 1 1/5?
A: No, they represent the same numerical value. 6/5 is an improper fraction, while 1 1/5 is a mixed number, but both are equivalent to 1.2. The choice of which form to use depends on the context of the problem.
Conclusion: Mastering Decimal-Fraction Conversion
Converting decimals to fractions is a crucial skill in mathematics. Understanding the underlying principles of place value and the relationship between decimals and fractions allows for a smooth and efficient conversion process. The example of 1.2, converted to 6/5 or 1 1/5, illustrates a fundamental mathematical concept that applies to a wide range of numbers. Remember the steps, practice with different decimals, and you'll master this essential skill in no time. The ability to seamlessly move between decimal and fraction representations enhances your mathematical fluency and problem-solving abilities. By understanding the intricacies of this conversion, you’re building a stronger foundation for more advanced mathematical concepts.
Latest Posts
Latest Posts
-
X 1 2 X 3
Sep 17, 2025
-
Citadel In Athens Crossword Clue
Sep 17, 2025
-
The Very Hungry Caterpillar Plot
Sep 17, 2025
-
Colors That Blend With Brown
Sep 17, 2025
-
Daily Horoscopes Sunday March 16th
Sep 17, 2025
Related Post
Thank you for visiting our website which covers about What's 1.2 As A Fraction . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.