X X 1 X 2
catronauts
Sep 11, 2025 · 6 min read
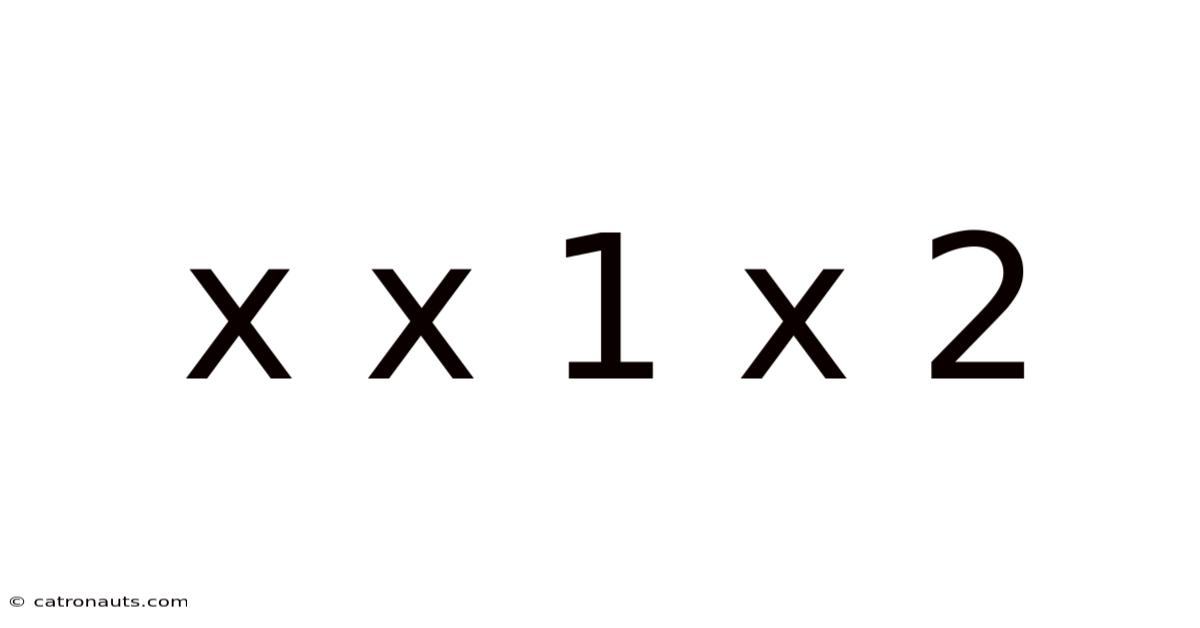
Table of Contents
Decoding the Mystery: A Deep Dive into x x 1 x 2
The seemingly simple sequence "x x 1 x 2" might initially appear cryptic, but it opens a door to a fascinating exploration of mathematics, logic, and pattern recognition. This seemingly simple sequence can represent various mathematical concepts, depending on the context. This article will delve into potential interpretations, explore underlying principles, and offer a comprehensive understanding of this intriguing sequence. We'll examine several possibilities, analyzing the inherent logic and the mathematical frameworks that could underpin such a pattern. This exploration will be beneficial for anyone interested in mathematics, problem-solving, and the beauty of hidden patterns.
Understanding the Variables: What Does 'x' Represent?
The key to unlocking the mystery lies in understanding the variable 'x'. It's not simply an unknown; it represents a placeholder for a value or a relationship waiting to be discovered. Depending on the context, 'x' could represent:
- An unknown number: The simplest interpretation is that 'x' represents an integer, and the sequence presents a partial arithmetic or geometric progression. We might need additional information or a specific problem to solve for 'x'.
- A variable in an equation: 'x' could be a component of a more complex mathematical equation where the sequence represents part of a larger pattern or solution.
- A symbol in a code or cipher: The sequence might be part of a code, where 'x' represents a specific letter or symbol, requiring decryption using cryptographic methods.
- A placeholder for an operation: Less likely, but possible, 'x' could represent a mathematical operation itself, requiring deeper investigation into the overall pattern's rules.
Potential Interpretations and Mathematical Frameworks
Let's explore several potential interpretations of the sequence "x x 1 x 2":
1. Arithmetic Progression:
If we assume 'x' represents a number, we could analyze this sequence as a partial arithmetic progression. This means there's a constant difference between consecutive terms. However, without more terms, determining if this is indeed an arithmetic progression is impossible. We could hypothesize different scenarios:
- Scenario A: The difference is 'x - 1'. In this case, the sequence might continue as x, x, 1, x-1, x-2, etc. This suggests 'x' must be greater than 2.
- Scenario B: The difference is '1 - x'. Here, the sequence could continue as x, x, 1, 1-x, 1-2x, etc. Again, the value of 'x' influences the subsequent terms.
- Scenario C: The difference isn't constant. This would invalidate the arithmetic progression hypothesis and require investigation into other mathematical frameworks.
2. Geometric Progression:
A geometric progression involves a constant ratio between consecutive terms. Applying this to our sequence, we encounter similar issues:
- We'd need additional terms to determine a constant ratio, and the value of 'x' would play a crucial role in defining that ratio.
- The presence of '1' and '2' complicates the matter significantly, as they represent distinct values that don't readily align with a consistent geometric ratio based on an unknown 'x'.
3. Fibonacci-like Sequences:
Fibonacci sequences are characterized by the sum of the two preceding terms defining the next term. While our sequence doesn't directly conform to the standard Fibonacci sequence (0, 1, 1, 2, 3, 5...), variations are possible. For example:
- A modified Fibonacci sequence could incorporate 'x' in its initial terms or rule. This would necessitate defining the precise way 'x' interacts with the summation process. Several unique Fibonacci-like sequences could be constructed depending on how 'x' is incorporated into the recursive rule.
4. Combinatorial or Permutational Approaches:
We could explore possibilities where 'x' represents the number of choices available at each stage of a combinatorial or permutational problem. However, without additional context, it's difficult to draw concrete conclusions. More information would be needed to determine if a specific combinatorial problem could be encoded in this format.
5. Contextual Clues:
The true meaning of "x x 1 x 2" hinges heavily on context. It could be:
- A coding problem: 'x' might represent a specific character or instruction, requiring knowledge of the specific coding language or cipher system.
- A puzzle: The sequence could be part of a larger puzzle that provides additional clues about 'x' and its role.
- A mathematical equation: The sequence could be a portion of a more substantial equation, where understanding the entire equation will reveal the significance of 'x'.
- A sequence in a game: 'x' might be a key variable in a game's rules or scoring system.
Advanced Mathematical Considerations
For more advanced analysis, we can incorporate concepts such as:
- Polynomials: Could the sequence be coefficients in a polynomial?
- Matrices: Could the sequence represent elements of a matrix?
- Recurrence Relations: A recurrence relation could define the sequence, with 'x' playing a key role in the recursive formula.
Solving for 'x': The Importance of Context
Ultimately, solving for 'x' requires more information. The sequence "x x 1 x 2" is not a self-contained mathematical problem; it's a fragment waiting for its context to be defined. This emphasizes the significance of the surrounding information in solving mathematical problems.
Practical Applications and Real-World Examples
The principles demonstrated in exploring the "x x 1 x 2" sequence have numerous applications in various fields:
- Cryptography: Understanding patterns and their underlying logic is critical in cryptography for both code-breaking and secure code design.
- Data Analysis: Identifying patterns in datasets is crucial for extracting meaningful insights and making predictions.
- Computer Science: Pattern recognition and algorithm design rely heavily on understanding sequence logic.
- Engineering: Solving complex engineering problems often involves identifying and utilizing underlying patterns.
Frequently Asked Questions (FAQ)
Q: Is there a single definitive answer to the meaning of "x x 1 x 2"?
A: No. Without additional context or information, there's no single definitive answer. The meaning depends entirely on the situation in which the sequence is presented.
Q: Can I use this sequence in a mathematical puzzle or code?
A: Absolutely! You can adapt and use this sequence in various ways, providing sufficient context for others to understand the intended meaning and rules. Make sure the puzzle or code is clear and well-defined.
Q: What are some common mistakes people make when analyzing sequences?
A: Assuming a single solution without considering other possibilities is a common mistake. Also, overlooking the importance of context and additional information can lead to incorrect conclusions.
Q: How can I improve my skills in pattern recognition?
A: Practice is key. Work through various mathematical puzzles, code-breaking exercises, and data analysis problems. Focus on understanding the underlying logic and principles behind each sequence.
Conclusion: The Power of Pattern Recognition
The seemingly simple sequence "x x 1 x 2" serves as a powerful illustration of the importance of context, pattern recognition, and logical deduction in mathematics and problem-solving. While the specific value of 'x' remains elusive without additional information, exploring the potential interpretations highlights the rich mathematical landscape that even simple sequences can unlock. The process of analyzing this sequence demonstrates the multifaceted nature of mathematical thinking, showcasing the beauty and power of pattern recognition and logical reasoning. By exploring this seemingly simple problem, we gain valuable insights into the broader world of mathematics and its pervasive influence across numerous fields. The journey of unraveling the mystery of "x x 1 x 2" is not just about finding a numerical solution; it's about developing a deeper appreciation for the elegance and versatility of mathematical concepts and their practical applications.
Latest Posts
Latest Posts
-
St George Coptic Orthodox Church
Sep 11, 2025
-
What Is Vertically Opposite Angle
Sep 11, 2025
-
Bund Sightseeing Tunnel Shanghai China
Sep 11, 2025
-
What Is 10 Of 250
Sep 11, 2025
-
Quotes From The Book Matilda
Sep 11, 2025
Related Post
Thank you for visiting our website which covers about X X 1 X 2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.